【题目】暑假期间,小明和小颖两家共8人相约外出旅行,分别乘坐两辆出租车前往机场在距离机场11千米处一辆车出了故障不能继续行驶.此时离机场停止办理登机手续还有30分钟,唯一可以利用的交通工具只有另一辆出租车,连同司机在内限乘5人,车速每小时60千米.
(1)如果这辆车分两批接送,其中4人乘车先走,余下4人原地等候,8人能否及时到达机场办理登机手续?(上下车时间忽略不计)
(2)如果这辆车在送第一批客人的时候,余下的人以每小时6千米的速度步行前往机场,待司机将第一批客人送达后立即返回接第二批客人,他们能及时到达机场吗?
参考答案:
【答案】(1)8人不能及时到达机场办理登记手续;(2)他们不能及时到达机场.
【解析】
(1)根据路程、速度、时间之间的等量关系即可求出答案;
(2)设余下的人共步行了x小时,然后根据题意给出的等量关系即可求出答案.
(1)由题意可知:汽车共走了3次全程,
即3×11=33千米,∴所有人到达机场共用了![]() 小时,即33分钟,故8人不能及时到达机场办理登记手续.
小时,即33分钟,故8人不能及时到达机场办理登记手续.
答:8人不能及时到达机场办理登记手续;
(2)设余下的人共步行了x小时,
所以汽车第一次到达机场再返回接余下的人时,共走了(60x﹣11)千米,∴6x+60x﹣11=11,
解得:x![]() ,
,
即余下的人共行了22分钟,∴从接到余下的人后,第二次到达机场共时间为:![]() 小时≈8.8分钟,
小时≈8.8分钟,
所以所有人达到机场共用了30.8分钟,也是不能及时到达机场,
答:在送第一批客人的时候,余下的人以每小时6千米的速度步行前往机场,待司机将第一批客人送达后立即返回接第二批客人,他们不能及时到达机场.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形纸片ABCD,AD=4,AB=3,如果点E在边BC上,将纸片沿AE折叠,使点B落在点F处,联结FC,当△EFC是直角三角形时,那么BE的长为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简
 ÷(
÷( -
- ),然后再从-2<x≤2的范围内选取一个合适的x的整数值代入求值
),然后再从-2<x≤2的范围内选取一个合适的x的整数值代入求值【答案】4.
【解析】试题分析:先将原分式进行化解,化解过程中注意不为0的量,根据不为0的量结合x的取值范围得出合适的x的值,将其代入化简后的代数式中即可得出结论.
试题解析:原式=
 =
= =
= .
.其中
 ,即x≠﹣1、0、1.
,即x≠﹣1、0、1.又∵﹣2<x≤2且x为整数,∴x=2.
将x=2代入
 中得:
中得: 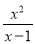 =
= =4.
=4.考点:分式的化简求值.
【题型】解答题
【结束】
21【题目】解方程:

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,己知抛物线y=k(x+1)(x﹣3k)(且k>0)与x轴分别交于A、B两点,A点在B点左边,与Y轴交于C点,连接BC,过A点作AE∥CB交抛物线于E点,0为坐标原点.
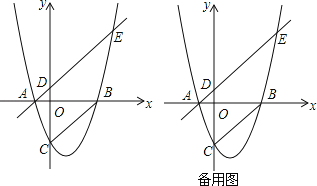
(1)用k表示点C的坐标(0, );
(2)若k=1,连接BE,
①求出点E的坐标;
②在x轴上找点P,使以P、B、C为顶点的三角形与△ABE相似,求出P点坐标;
(3)若在直线AE上存在唯一的一点Q,连接OQ、BQ,使OQ⊥BQ,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
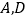 是一段圆弧上的两点,且在直线
是一段圆弧上的两点,且在直线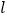 的同侧,分别过这两点作
的同侧,分别过这两点作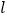 的垂线,垂足为
的垂线,垂足为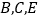 是
是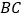 上一动点,连接
上一动点,连接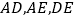 ,且
,且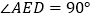 .
.(1)如图①,如果
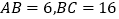 ,且
,且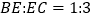 ,求
,求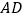 的长;
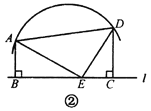
的长;(2)如图②,若点
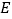 恰为这段圆弧的圆心,则线段
恰为这段圆弧的圆心,则线段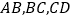 之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当
之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当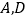 分别在直线
分别在直线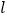 两侧且
两侧且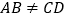 ,而其余条件
,而其余条件不变时,线段
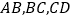 之间又有怎样的等量关系?请直接写出结论,不必证明.
之间又有怎样的等量关系?请直接写出结论,不必证明.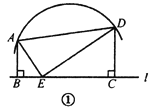
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,⊙C的半径为r(r>1),P是圆内与圆心C不重合的点,⊙C的“完美点”的定义如下:若直线CP与⊙C交于点A,B,满足|PA-PB|=2,则称点P为⊙C的“完美点”,如图为⊙C及其“完美点”P的示意图.
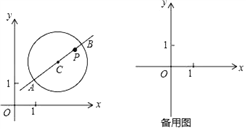
(1)当⊙O的半径为2时,
①点M(
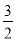 ,0) ⊙O的“完美点”,点N(0,1) ⊙O的“完美点”,点T(-
,0) ⊙O的“完美点”,点N(0,1) ⊙O的“完美点”,点T(-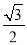 ,-
,- 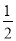 ) ⊙O的“完美点”(填“是”或者“不是”);
) ⊙O的“完美点”(填“是”或者“不是”);②若⊙O的“完美点”P在直线y=
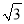 x上,求PO的长及点P的坐标;
x上,求PO的长及点P的坐标;(2)⊙C的圆心在直线y=
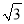 x+1上,半径为2,若y轴上存在⊙C的“完美点”,求圆心C的纵坐标t的取值范围.
x+1上,半径为2,若y轴上存在⊙C的“完美点”,求圆心C的纵坐标t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制了如下尚不完整的统计图表:
调查结果统计表

调查结果频数分布直方图 调查结果扇形统计图

请根据以上图表,解答下列问题:
(1)填空:这次调查的样本容量是 ,
 ,
, ;
;(2)补全频数分布直方图;
(3)求扇形统计图中扇形
 的圆心角度数;
的圆心角度数;(4)该校共有
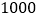 人,请估计每月零花钱的数额
人,请估计每月零花钱的数额 在
在 范围的人数.
范围的人数.
相关试题

