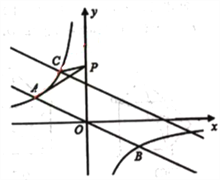
【题目】如图,直角坐标系中,直线![]() 与反比例函数
与反比例函数![]() 的图象交于A,B两点,已知A点的纵坐标是2.
的图象交于A,B两点,已知A点的纵坐标是2.
(1)求反比例函数的解析式.
(2)将直线![]() 沿x轴向右平移6个单位后,与反比例函数在第二象限内交于点C.动点P在y轴正半轴上运动,当线段PA与线段PC之差达到最大时,求点P的坐标.
沿x轴向右平移6个单位后,与反比例函数在第二象限内交于点C.动点P在y轴正半轴上运动,当线段PA与线段PC之差达到最大时,求点P的坐标.
参考答案:
【答案】(1)![]() ;(2)P(0,6)
;(2)P(0,6)
【解析】试题分析:(1)先求得点A的坐标,再利用待定系数法求得反比例函数的解析式即可;(2)连接AC,根据三角形两边之差小于第三边知:当A、C、P不共线时,PA-PC<AC;当A、C、P不共线时,PA-PC=AC;因此,当点P在直线AC与y轴的交点时,PA-PC取得最大值.先求得平移后直线的解析式,再求得平移后直线与反比例函数的图象的交点坐标,最后求直线AC的解析式,即可求得点P的坐标.
试题解析:
![]() 令一次函数
令一次函数![]() 中
中![]() ,则
,则![]() ,
,
解得:![]() ,即点A的坐标为(-4,2).
,即点A的坐标为(-4,2).
∵点A(-4,2)在反比例函数![]() 的图象上,
的图象上,
∴k=-4×2=-8,
∴反比例函数的表达式为![]() .
.
![]() 连接AC,根据三角形两边之差小于第三边知:当A、C、P不共线时,PA-PC<AC;当A、C、P不共线时,PA-PC=AC;因此,当点P在直线AC与y轴的交点时,PA-PC取得最大值.
连接AC,根据三角形两边之差小于第三边知:当A、C、P不共线时,PA-PC<AC;当A、C、P不共线时,PA-PC=AC;因此,当点P在直线AC与y轴的交点时,PA-PC取得最大值.
设平移后直线于x轴交于点F,则F(6,0)
设平移后的直线解析式为![]() ,
,
将F(6,0)代入![]() 得:b=3
得:b=3
∴直线CF解析式:![]()
令![]() 3=
3=![]() ,解得:
,解得:![]() ,
,
∴C(-2,4)
∵A、C两点坐标分别为A(-4,2)、C(-2,4)
∴直线AC的表达式为![]() ,
,
此时,P点坐标为P(0,6).
-
科目: 来源: 题型:
查看答案和解析>>【题目】“校园安全”受到全社会的广泛关注,东营市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
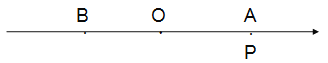
(1)写出数轴上点B表示的数 _______,点P表示的数________(用含t的代数式表示);
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?(5分)
(3)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长;(5分)
(4)若点D是数轴上一点,点D表示的数是x,请你探索式子|x+6|+|x-8|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.(5分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
调查结果统计表
组别
分组(单位:元)
人数
A
0≤x<30
4
B
30≤x<60
16
C
60≤x<90
a
D
90≤x<120
b
E
x≥120
2
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__人,a+b=__,m=___;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额x在60≤x<120范围的人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】暑假期间,小明和小颖两家共8人相约外出旅行,分别乘坐两辆出租车前往机场在距离机场11千米处一辆车出了故障不能继续行驶.此时离机场停止办理登机手续还有30分钟,唯一可以利用的交通工具只有另一辆出租车,连同司机在内限乘5人,车速每小时60千米.
(1)如果这辆车分两批接送,其中4人乘车先走,余下4人原地等候,8人能否及时到达机场办理登机手续?(上下车时间忽略不计)
(2)如果这辆车在送第一批客人的时候,余下的人以每小时6千米的速度步行前往机场,待司机将第一批客人送达后立即返回接第二批客人,他们能及时到达机场吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.
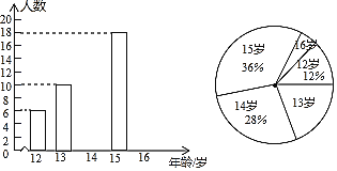
依据以上信息解答以下问题:
(1)分别求出14岁和16岁的学生人数,并补全条形统计图;
(2)这个样本的众数是_____岁,中位数是_____岁;
(3)若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=50°,过点O引射线OC,若∠AOC:∠BOC=2:3,OD平分∠AOB,求∠COD的度数.

相关试题

