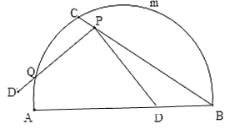
【题目】如图,C是![]() 的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转
的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转![]() 得到线段
得到线段![]() .射线
.射线![]() 与
与![]() 交于点Q.已知
交于点Q.已知![]() ,设P,C两点间的距离为xcm,P,D两点间的距离
,设P,C两点间的距离为xcm,P,D两点间的距离![]() ,P,Q两点的距离为
,P,Q两点的距离为![]() .
.
小石根据学习函数的经验,分别对函数![]() ,
,![]() ,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() ,
,![]() ,与x的几组对应值:
,与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4.29 | 3.33 | 1.65 | 1.22 | 1.0 | 2.24 | |
| 0.88 | 2.84 | 3.57 | 4.04 | 4.17 | 3.20 | 0.98 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数据所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
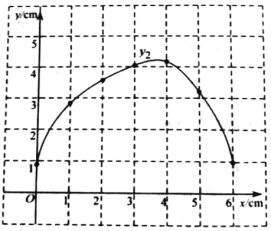
(3)结合函数图象,解决问题:连接DQ,当△DPQ为等腰三角形时,PC的长度约为_____cm.(结果保留一位小数)
参考答案:
【答案】(1)2.36;(2)见解析;(3)1.26或5.84
【解析】
(1)测量出PC=2cm时,PD的值,填入表格即可即可;
(2)根据表格数据描点,圆平滑曲线连接即可;
(3)由△DPQ是等腰三角形可得PD=PQ,即y1=y2,根据图象找出两个图象的交点,即可得x的值,即PC的大约长度.
(1)经过测量,当PC=2cm时,PD=2.36cm,
故答案为:2.36
(2)函数y1、y2的图象如图所示:
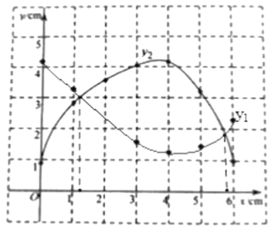
(3)∵△DPQ是等腰三角形,
∴PD=PQ,即y1=y2,
由图象可知:y1=y2时,x≈1.26或x≈5.84,
∴PC的长度约为1.26cm或5.84cm,
故答案为:1.26或5.84
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x
学校
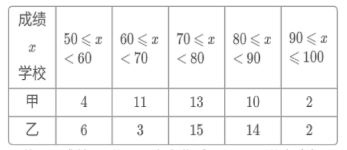

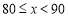

甲
4
11
13
10
2
乙
6
3
15
14
2
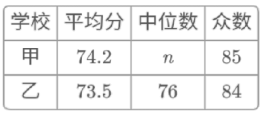
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在
 这一组的是:
这一组的是:70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校
平均分
中位数
众数
甲
74.2
n
5
乙
73.5
76
84
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
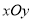 中,直线
中,直线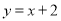 与函数
与函数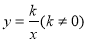 的图象交于
的图象交于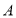 ,
,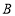 两点,且点
两点,且点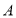 的坐标为
的坐标为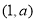 .
.
(1)求
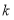 的值;
的值;(2)已知点
 ,过点
,过点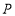 作平行于
作平行于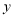 轴的直线,交直线
轴的直线,交直线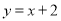 于点
于点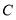 ,交函数
,交函数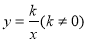 的图象于点
的图象于点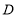 .
.①当
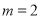 时,求线段
时,求线段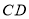 的长;
的长;②若
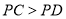 ,结合函数的图象,直接写出
,结合函数的图象,直接写出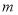 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ACB中,∠C=90°,AC=3,BC=4,O是BC的中点,到点O的距离等于
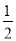 BC的所有点组成的图形记为G,图形G与AB交于点D.
BC的所有点组成的图形记为G,图形G与AB交于点D.
(1)补全图形并求线段AD的长;
(2)点E是线段AC上的一点,当点E在什么位置时,直线ED与 图形G有且只有一个交点?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
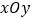 中,直线
中,直线 与
与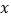 轴、
轴、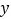 轴分别交于点
轴分别交于点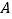 ,
,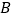 ,抛物线
,抛物线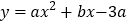 经过点
经过点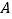 ,将点
,将点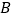 向右平移5个单位长度,得到点
向右平移5个单位长度,得到点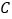 .
.(1)求点
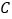 的坐标;
的坐标;(2)求抛物线的对称轴;
(3)若抛物线与线段
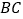 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求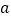 的取值范围.
的取值范围. -
科目: 来源: 题型:
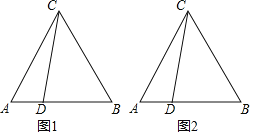
查看答案和解析>>【题目】已知△ABC为等边三角形,点D是线段AB上一点(不与A、B重合).将线段CD绕点C逆时针旋转60°得到线段CE.连结DE、BE.
(1)依题意补全图1并判断AD与BE的数量关系.
(2)过点A作AF⊥EB交EB延长线于点F.用等式表示线段EB、DB与AF之间的数量关系并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,⊙O的半径为r(r>0).给出如下定义:若平面上一点P到圆心O的距离d,满足
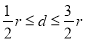 ,则称点P为⊙O的“随心点”.
,则称点P为⊙O的“随心点”.
(1)当⊙O的半径r=2时,A(3,0),B(0,4),C(
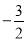 ,2),D(
,2),D(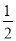 ,
,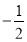 )中,⊙O的“随心点”是 ;
)中,⊙O的“随心点”是 ;(2)若点E(4,3)是⊙O的“随心点”,求⊙O的半径r的取值范围;
(3)当⊙O的半径r=2时,直线y=- x+b(b≠0)与x轴交于点M,与y轴交于点N,若线段MN上存在⊙O的“随心点”,直接写出b的取值范围 .
相关试题

