【题目】在平面直角坐标系xOy中,⊙O的半径为r(r>0).给出如下定义:若平面上一点P到圆心O的距离d,满足![]() ,则称点P为⊙O的“随心点”.
,则称点P为⊙O的“随心点”.
(1)当⊙O的半径r=2时,A(3,0),B(0,4),C(![]() ,2),D(
,2),D(![]() ,
,![]() )中,⊙O的“随心点”是 ;
)中,⊙O的“随心点”是 ;
(2)若点E(4,3)是⊙O的“随心点”,求⊙O的半径r的取值范围;
(3)当⊙O的半径r=2时,直线y=- x+b(b≠0)与x轴交于点M,与y轴交于点N,若线段MN上存在⊙O的“随心点”,直接写出b的取值范围 .
参考答案:
【答案】(1) A,C ;(2)![]() ;(3) 1≤b≤
;(3) 1≤b≤![]() 或-
或-![]() ≤b≤-1.
≤b≤-1.
【解析】
(1)根据已知条件求出d的范围:1≤d≤3,再将各点距离O点的距离,进行判断是否在此范围内即可,满足条件的即为随心点;
(2)根据点E(4,3)是⊙O的“随心点”,可根据![]() ,求出d=5,再求出r的范围即可;
,求出d=5,再求出r的范围即可;
(3)如图a∥b∥c∥d,⊙O的半径r=2,求出随心点范围![]() ,再分情况点N在y轴正半轴时,当点N在y轴负半轴时,分情况讨论即可.
,再分情况点N在y轴正半轴时,当点N在y轴负半轴时,分情况讨论即可.
(1) ∵⊙O的半径r=2,
∴![]() =3,
=3,![]() =1
=1
∴1≤d≤3
∵A(3,0),
∴OA=3,在范围内
∴点A是⊙O的“随心点”
∵B(0,4)
∴OB=4,而4>3,不在范围内
∴B是不是⊙O的“随心点”,
∵C(![]() ,2),
,2),
∴OC=![]() ,在范围内
,在范围内
∴点C是⊙O的“随心点”,
∵D(![]() ,
,![]() ),
),
∴OD=![]() <1,不在范围内
<1,不在范围内
∴点D不是⊙O的“随心点”,
故答案为:A,C
(2)∵点E(4,3)是⊙O的“随心点”
∴OE=5,即d=5
若![]() , ∴r=10
, ∴r=10
若 ![]() ,
,![]()
∴![]()
(3)
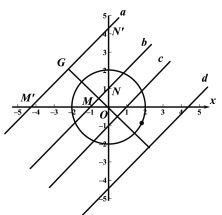
∵如图a∥b∥c∥d,⊙O的半径r=2,随心点范围![]()
∴![]()
∵直线MN的解析式为y=x+b,
∴OM=ON,
①点N在y轴正半轴时,
当点M是⊙O的“随心点”,此时,点M(-1,0),
将M(-1,0)代入直线MN的解析式y=x+b中,解得,b=1,
即:b的最小值为1,
过点O作OG⊥M'N'于G,
当点G是⊙O的“随心点”时,此时OG=3,
在Rt△ON'G中,∠ON'G=45°,
∴GO=3
∴在Rt△GNN’中,![]() =
=![]() =
=![]() =
=![]() ,
,
b的最大值为![]() ,
,
∴1≤b≤![]() ,
,
②当点N在y轴负半轴时,同①的方法得出-![]() ≤b≤-1.
≤b≤-1.
综上所述,b的取值范围是:1≤b≤![]() 或-
或-![]() ≤b≤-1.
≤b≤-1.
-
科目: 来源: 题型:
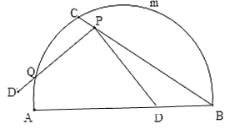
查看答案和解析>>【题目】如图,C是
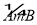 的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转
的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转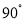 得到线段
得到线段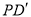 .射线
.射线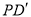 与
与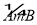 交于点Q.已知
交于点Q.已知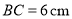 ,设P,C两点间的距离为xcm,P,D两点间的距离
,设P,C两点间的距离为xcm,P,D两点间的距离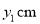 ,P,Q两点的距离为
,P,Q两点的距离为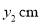 .
.
小石根据学习函数的经验,分别对函数
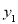 ,
,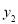 ,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了
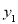 ,
,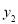 ,与x的几组对应值:
,与x的几组对应值:x/cm
0
1
2
3
4
5
6
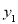 /cm
/cm4.29
3.33
1.65
1.22
1.0
2.24
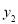 /cm
/cm0.88
2.84
3.57
4.04
4.17
3.20
0.98
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数据所对应的点
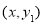 ,
,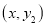 ,并画出函数
,并画出函数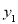 ,
, 的图象;
的图象;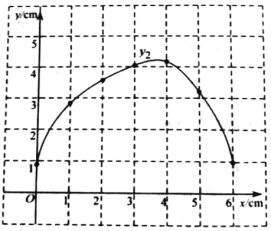
(3)结合函数图象,解决问题:连接DQ,当△DPQ为等腰三角形时,PC的长度约为_____cm.(结果保留一位小数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
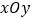 中,直线
中,直线 与
与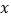 轴、
轴、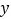 轴分别交于点
轴分别交于点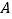 ,
,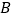 ,抛物线
,抛物线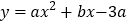 经过点
经过点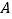 ,将点
,将点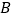 向右平移5个单位长度,得到点
向右平移5个单位长度,得到点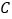 .
.(1)求点
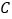 的坐标;
的坐标;(2)求抛物线的对称轴;
(3)若抛物线与线段
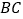 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求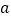 的取值范围.
的取值范围. -
科目: 来源: 题型:
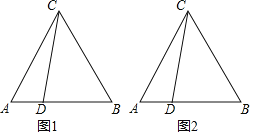
查看答案和解析>>【题目】已知△ABC为等边三角形,点D是线段AB上一点(不与A、B重合).将线段CD绕点C逆时针旋转60°得到线段CE.连结DE、BE.
(1)依题意补全图1并判断AD与BE的数量关系.
(2)过点A作AF⊥EB交EB延长线于点F.用等式表示线段EB、DB与AF之间的数量关系并证明.
-
科目: 来源: 题型:
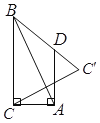
查看答案和解析>>【题目】如图,在
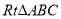 中,
中,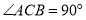 ,作
,作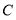 点关于直线
点关于直线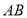 的对称点
的对称点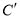 ,连接
,连接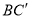 .过
.过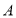 点作
点作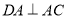 交
交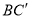 于点
于点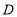 ,若
,若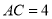
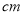 ,
,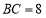
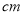 ,则
,则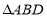 的周长是_____
的周长是_____ 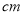 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明在家乡的楼顶上
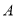 处测得池塘的一端
处测得池塘的一端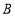 处的俯角为
处的俯角为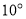 ,测得池塘
,测得池塘 处的俯角
处的俯角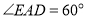 ,
,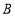 、
、 、
、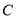 三点在同一水平直线上.已知楼高
三点在同一水平直线上.已知楼高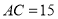 米,求池塘宽
米,求池塘宽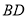 为多少米?(参考数据:
为多少米?(参考数据: ,
,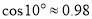 ,
, 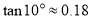 ,
,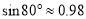 ,
,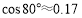 ,
, 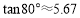 ,
,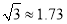 .结果保留一位小数.)
.结果保留一位小数.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年世界杯足球赛的“大力神杯”系列纪念品是中国制造.某商店用10000元购进一批“大力神杯”钥匙扣进行销售,很快销售一空.然后商店又用24000元购进这种钥匙扣,所购数量是第一批购进数量的2倍,但每个钥匙扣的价格比第一批的价格多了2元.
(1)该商店第一批购进的钥匙扣单价是多少元?
(2)若该商店第一、二批购进的钥匙扣都按相同的标价出售,并且全部售完,要使利润不低于20%,则每个钥匙扣的标价至少是多少元?
(3)在销售第二批钥匙扣时发现,若以每个15元价格出售,可全部售完.每涨价1元,销售量减少100件,剩余钥匙扣以每个10元价格全部售出.设该商店在销售第二批钥匙扣所获利润为P元,销售单价为m元,求P与m的函数关系式,并求出利润P最大时m的值.
相关试题

