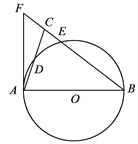
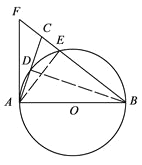
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=![]() ,
, ![]() ,求BE的长.
,求BE的长.
参考答案:
【答案】(1)证明见解析;(2)BE的长为8.
【解析】分析:(1)首先连接BD,由AB为直径,可得∠ADB=90°,又由AF是 O的切线,易证得∠CAF=∠ABD.然后由BA=BC,证得:∠ABC=2∠CAF;
(2)连接AE,利用已知条件分别求出BC,CE的长,由BE=BC-CE计算即可.
本题解析:
(1)证明:连结BD.∵AB是![]() 的直径,∴∠ADB=90°.∴∠DAB+∠DBA=90°.∵AB=AC,∴2∠ABD=∠ABC,AD=
的直径,∴∠ADB=90°.∴∠DAB+∠DBA=90°.∵AB=AC,∴2∠ABD=∠ABC,AD=![]() AC.∵AF为⊙O的切线,∴∠FAB=90°.∴∠FAC+∠CAB=90°.∴∠FAC=∠ABD, ∠ABC=2∠CAF.
AC.∵AF为⊙O的切线,∴∠FAB=90°.∴∠FAC+∠CAB=90°.∴∠FAC=∠ABD, ∠ABC=2∠CAF.
(2)解:连接AE.∴∠AEB=∠AEC=90°.∵sin∠CAF=![]() , ∠ABD=∠CAF=∠CBD=∠CAE∴sin∠ABD=sin∠CAF=
, ∠ABD=∠CAF=∠CBD=∠CAE∴sin∠ABD=sin∠CAF=![]() .∵∠ABD=90°,AC=2
.∵∠ABD=90°,AC=2![]() ,∴AD=
,∴AD=![]() ,AB=
,AB=![]() =10.∵∠AEC=90°,AC=2
=10.∵∠AEC=90°,AC=2![]() ,∴CE=AC·sin∠CAE=2 , ∴BE=BC-CE=10-2=8.
,∴CE=AC·sin∠CAE=2 , ∴BE=BC-CE=10-2=8. 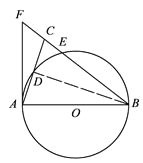
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直线上顺次取A,B,C三点,分别以AB,BC为边长在直线的同侧作正三角形,作得两个正三角形的另一顶点分别为D,E.
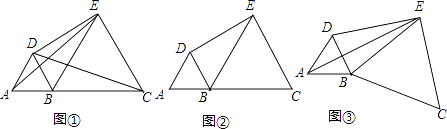
(1)如图①,连结CD,AE,求证:CD=AE;
(2)如图②,若AB=1,BC=2,求DE的长;
(3)如图③,将图②中的正三角形BEC绕B点作适当的旋转,连结AE,若有DE2+BE2=AE2 , 试求∠DEB的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】A(0,4)是直角坐标系y轴上一点,P是x轴上一动点,从原点O出发,沿正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.
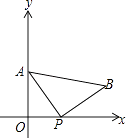
(1)若AB∥x轴,求t的值;
(2)设点B的坐标为(x,y),试求y关于x的函数表达式;
(3)当t=3时,平面直角坐标系内有一点M(3,a),请直接写出使△APM为等腰三角形的点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个等腰三角形的两边长分别为2和4,则该等腰三角形的周长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1)(4a2﹣3a)﹣(2a2+a﹣1),其中a=4.
(2)已知m、n互为倒数,求:﹣2(mn﹣3m2)﹣m2+5 (mn﹣m2)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点P(a+1,a-1)在x轴上,那么点P的坐标为( )
A. (-2,0) B. (2,0) C. (0,-2) D. (0,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)化简后再求值:
 ,其中
,其中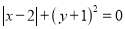
(2)若关于x、y的单项式cx2a+2y2与0.4xy3b+4的和为零,则
 a2b-[
a2b-[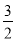 a2b-(3abc-a2c)-4a2c]-3abc的值又是多少?
a2b-(3abc-a2c)-4a2c]-3abc的值又是多少?
相关试题

