【题目】A(0,4)是直角坐标系y轴上一点,P是x轴上一动点,从原点O出发,沿正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.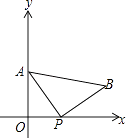
(1)若AB∥x轴,求t的值;
(2)设点B的坐标为(x,y),试求y关于x的函数表达式;
(3)当t=3时,平面直角坐标系内有一点M(3,a),请直接写出使△APM为等腰三角形的点M的坐标.
参考答案:
【答案】
(1)
解:过点B作BC⊥x轴于点C,如图1所示.
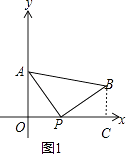
∵AO⊥x轴,BC⊥x轴,且AB∥x轴,
∴四边形ABCO为长方形,
∴AO=BC=4.
∵△APB为等腰直角三角形,
∴AP=BP,∠PAB=∠PBA=45°,
∴∠OAP=90°﹣∠PAB=45°,
∴△AOP为等腰直角三角形,
∴OA=OP=4.
t=4÷1=4(秒),
故t的值为4
(2)
解:∵△APB为等腰直角三角形,
∴∠APO+∠BPC=180°﹣90°=90°.
又∵∠PAO+∠APO=90°,
∴∠PAO=∠BPC.
在△PAO和△BPC中, 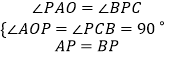 ,
,
∴△PAO≌△BPC,
∴AO=PC,BC=PO.
∵点A(0,4),点P(t,0),点B(x,y),
∴PC=AO=4,BC=PO=t=y,CO=PC+PO=4+y=x,
∴y=x﹣4
(3)
解:△APM为等腰三角形分三种情况:
①当AM=AP时,如图2所示.
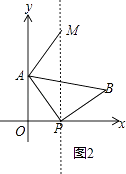
当t=3时,点P(3,0),
∵点M(3,a),点A(0,4),
∴由两点间的距离公式可知:
AM= ![]() ,AP=
,AP= ![]() =5,
=5,
∴ ![]() =5,解得:a=0(舍去),a=8.
=5,解得:a=0(舍去),a=8.
此时M点的坐标为(3,8);
②当MA=MP时,如图3所示.
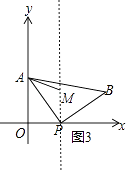
∵点P(3,0),点A(0,4),点M(3,a),
∴由两点间的距离公式可知:
MA= ![]() ,MP=a,
,MP=a,
∴ ![]() =a,解得:a=
=a,解得:a= ![]() .
.
此时M点的坐标为(3, ![]() );
);
③当PA=PM时,如图4所示.
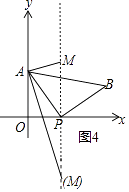
∵点P(3,0),点A(0,4),点M(3,a),
∴由两点间的距离公式可知:
PA= ![]() =5,PM=|a|,
=5,PM=|a|,
∴a=±5.
此时M点的坐标为(3,5)或(3,﹣5).
综上可知:当t=3时,平面直角坐标系内有一点M(3,a),使△APM为等腰三角形的点M的坐标为(3,8),(3, ![]() ),(3,5)和(3,﹣5)
),(3,5)和(3,﹣5)
【解析】(1)由AB∥x轴,可找出四边形ABCO为长方形,再根据△APB为等腰三角形可得知∠OAP=45°,从而得出△AOP为等腰直角三角形,由此得出结论;(2)先证出△PAO≌△BPC,即可得出各边的关系,利用坐标系中点的意义即可得出个线段的长度,由相等的量可得出结论;(3)由等腰三角形的性质可知,若△APM为等腰三角形只需找到一组临边相等即可,临边相等分三种情况,分类讨论结合两点间的距离公式即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出数轴上比-5大的所有负整数
-
科目: 来源: 题型:
查看答案和解析>>【题目】设一列数
 、
、 、
、 、…、 a2010中任意三个相邻数之和都是35,已知a3=2x,a20=15,
、…、 a2010中任意三个相邻数之和都是35,已知a3=2x,a20=15,  ,那么a2011=_________________。
,那么a2011=_________________。 -
科目: 来源: 题型:
查看答案和解析>>【题目】在直线上顺次取A,B,C三点,分别以AB,BC为边长在直线的同侧作正三角形,作得两个正三角形的另一顶点分别为D,E.
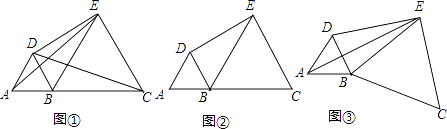
(1)如图①,连结CD,AE,求证:CD=AE;
(2)如图②,若AB=1,BC=2,求DE的长;
(3)如图③,将图②中的正三角形BEC绕B点作适当的旋转,连结AE,若有DE2+BE2=AE2 , 试求∠DEB的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个等腰三角形的两边长分别为2和4,则该等腰三角形的周长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=
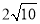 ,
, 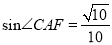 ,求BE的长.
,求BE的长.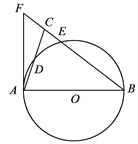
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1)(4a2﹣3a)﹣(2a2+a﹣1),其中a=4.
(2)已知m、n互为倒数,求:﹣2(mn﹣3m2)﹣m2+5 (mn﹣m2)的值.
相关试题

