搜索
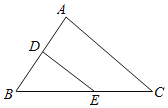
【题目】如图，在△ABC中、D、E分别是AB，BC上任意一点，连结DE，若BD＝4，DE＝5．
（1）BE的取值范围 ；
（2）若DE∥AC，∠A＝85°，∠BED＝35°，求∠B的度数．
参考答案：
【答案】（1）1＜BE＜9；（2）60°．
【解析】
（1）根据三角形的三边关系即可得出结论；
（2）根据平行线的性质，即可得到∠BED＝∠C＝35°，然后根据三角形的内角和定理即可求出∠B的度数．
解：（1）∵BD＝4，DE＝5，
∴△BDE中，5﹣4＜BE＜5+4，
即1＜BE＜9，
即BE的取值范围为：1＜BE＜9；
故答案为：1＜BE＜9；
（2）∵DE∥AC，
∴∠BED＝∠C＝35°，
又∵∠A＝85°，
∴△ABC中，∠B＝180°﹣∠A﹣∠C＝180°﹣85°﹣35°＝60°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1、2，已知四边形ABCD为正方形，在射线AC上有一动点P，作PE⊥AD（或延长线）于E，作PF⊥DC（或延长线）于F，作射线BP交EF于G．
（1）在图1中，设正方形ABCD的边长为2，四边形ABFE的面积为y，AP=x，求y关于x的函数表达式；
（2）结论：GB⊥EF对图1，图2都是成立的，请任选一图形给出证明；
（3）请根据图2证明：△FGC∽△PFB．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，某超市从一楼到二楼有一自动扶梯，图2是侧面示意图．已知自动扶梯AB的坡度为1：2．4，AB的长度是13米，MN是二楼楼顶，MN∥PQ，C是MN上处在自动扶梯顶端B点正上方的一点，BC⊥MN，在自动扶梯底端A处测得C点的仰角为42°，求二楼的层高BC约为多少米？（ sin42°≈0．7，tan42°≈0．9）
-
科目： 来源： 题型：
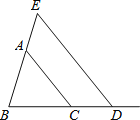
查看答案和解析>>【题目】如图，已知△ABC．
（1）若AB=4，AC=5，则BC边的取值范围是 ；
（2）点D为BC延长线上一点，过点D作DE∥AC，交BA的延长线于点E，若∠E=55°，∠ACD=125°，求∠B的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】随着新能源汽车推广力度加大，产业快速发展，越来越多的消费者接受并购买新能源汽车。我市某品牌新能源汽车经销商1月至3月份统计，该品牌汽车1月份销售150辆，3月份销售216辆.
（1）求该品牌新能源汽车销售量的月均增长率；
（2）若该品牌新能源汽车的进价为52000元，售价为58000元，则该经销商1月至3月份共盈利多少元？
-
科目： 来源： 题型：
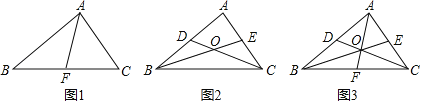
查看答案和解析>>【题目】问题解决：如图1，△ABC中，AF为BC边上的中线，则S△ABF＝ S△ABC．
问题探究：
（1）如图2，CD，BE分别是△ABC的中线，S△BOC与S四边形ADOE相等吗？
解：△ABC中，由问题解决的结论可得，S△BCD＝
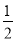S△ABC，S△ABE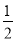＝S△ABC．∴S△BCD＝S△ABE
∴S△BCD﹣S△BOD＝S△ABE﹣S△BOD
即S△BOC＝S四边形ADOE．
（2）图2中，仿照（1）的方法，试说明S△BOD＝S△COE．
（3）如图3，CD，BE，AF分别是△ABC的中线，则S△BOC＝ S△ABC，S△AOE＝ S△ABC，S△BOD＝ S△ABF．
问题拓展：
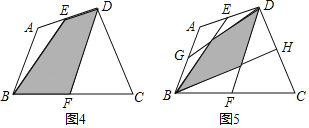
（4）①如图4，E、F分别为四边形ABCD的边AD、BC的中点，请直接写出阴影部分的面积与四边形ABCD的面积之间的数量关系：S阴影＝ S四边形ABCD．
②如图5，E、F、G、H分别为四边形ABCD的边AD、BC、AB、CD的中点，请直接写出阴影部分的面积与四边形ABCD的面积之间的数量关系：S阴影＝ S四边形ABCD．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图两个4×4网格都是由16个边长为1的小正方形组成．
(1)图①中的阴影正方形的顶点在网格的格点上，这个阴影正方形的面积为 ，若这个正方形的边长为
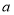，则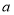＝ ；(2)请在图②中画出面积是5的正方形，使它的顶点在网格的格点上.若这个正方形的边长为
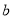，则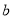＝ ；(3)请你利用以上结论，在 图③ 的数轴上精确画出实数
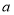和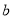－，利用数轴可得
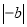.（填“﹥”或“﹤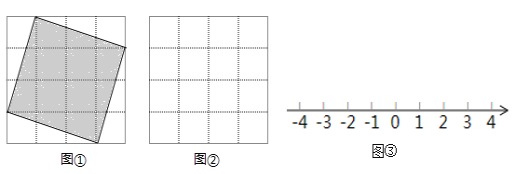
相关试题
