【题目】如图1、2,已知四边形ABCD为正方形,在射线AC上有一动点P,作PE⊥AD(或延长线)于E,作PF⊥DC(或延长线)于F,作射线BP交EF于G.
(1)在图1中,设正方形ABCD的边长为2,四边形ABFE的面积为y,AP=x,求y关于x的函数表达式;
(2)结论:GB⊥EF对图1,图2都是成立的,请任选一图形给出证明;
(3)请根据图2证明:△FGC∽△PFB.

参考答案:
【答案】(1)y=x2+2;(2)证明见解析;(3)证明见解析.
【解析】
试题分析:(1)根据题意得出S四边形ABFE=4﹣ED×DF﹣BC×FC进而得出答案;
(2)首先利用正方形的性质进而证明△FPE≌△BHP(SAS),即可得出△FPG∽△BPH,求出即可;
(3)首先得出△DPC≌△BPC(SAS),进而利用相似三角形的判定得出△FGC∽△PFB.
试题解析:(1)解:∵PE⊥AD,PF⊥DC,
∴四边形EPFD是矩形,
∵AP=x,
∴AE=EP=DF=![]() x,
x,
DE=PF=FC=2﹣![]() x,
x,
∴S四边形ABFE=4﹣EDDF﹣BCFC=x2+2;
(2)证明:如图1,延长FP交AB于H,
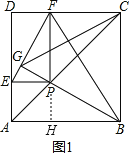
∵PF⊥DC,PE⊥AD,
∴PF⊥PE,PH⊥HB,
即∠BHP=90°,
∵四边形ABCD是正方形,
∴AC平分∠DAB,
∴可得PF=FC=HB,EP=PH,
在△FPE与△BHP中
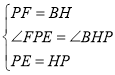 ,
,
∴△FPE≌△BHP(SAS),
∴∠PFE=∠PBH,
又∵∠FPG=∠BPH,
∴△FPG∽△BPH,
∴∠FGP=∠BHP=90°,
即GB⊥EF;
(3)证明:如图2,连接PD,

∵GB⊥EF,
∴∠BPF=∠CFG①,
在△DPC和△BPC中
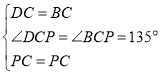 ,
,
∴△DPC≌△BPC(SAS),
∴PD=PB,
而PD=EF,∴EF=PB,
又∵GB⊥EF,
∴PF2=FGEF,
∴PF2=FGPB,
而PF=FC,
∴PFFC=FGPB,
∴![]() ②,
②,
∴由①②得△FGC∽△PFB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
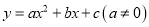 的部分图象如图,图象过点(﹣1,0),对称轴为直线
的部分图象如图,图象过点(﹣1,0),对称轴为直线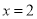 ,下列结论:①
,下列结论:①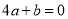 ;②
;②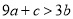 ;③
;③ ;④当
;④当 时,
时,  随
随 的增大而增大.其中正确的结论有( )
的增大而增大.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标,并画出△A1B1C1;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标,并画出△A3B3C3.

-
科目: 来源: 题型:
查看答案和解析>>【题目】随着改革开放进程的推进,改变的不仅仅是人们的购物模式,就连支付方式也在时代的浪潮中发生着天翻地覆的改变,除了现金、银行卡支付以外,还有微信、支付宝以及其他支付方式.在一次购物中,小明和小亮都想从微信、支付宝、银行卡三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC约为多少米?( sin42°≈0.7,tan42°≈0.9)

-
科目: 来源: 题型:
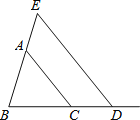
查看答案和解析>>【题目】如图,已知△ABC.
(1)若AB=4,AC=5,则BC边的取值范围是 ;
(2)点D为BC延长线上一点,过点D作DE∥AC,交BA的延长线于点E,若∠E=55°,∠ACD=125°,求∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中、D、E分别是AB,BC上任意一点,连结DE,若BD=4,DE=5.
(1)BE的取值范围 ;
(2)若DE∥AC,∠A=85°,∠BED=35°,求∠B的度数.
相关试题

