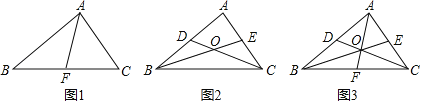
【题目】问题解决:如图1,△ABC中,AF为BC边上的中线,则S△ABF= S△ABC.
问题探究:
(1)如图2,CD,BE分别是△ABC的中线,S△BOC与S四边形ADOE相等吗?
解:△ABC中,由问题解决的结论可得,S△BCD=![]() S△ABC,S△ABE=
S△ABC,S△ABE=![]() S△ABC.
S△ABC.
∴S△BCD=S△ABE
∴S△BCD﹣S△BOD=S△ABE﹣S△BOD
即S△BOC=S四边形ADOE.
(2)图2中,仿照(1)的方法,试说明S△BOD=S△COE.
(3)如图3,CD,BE,AF分别是△ABC的中线,则S△BOC= S△ABC,S△AOE= S△ABC,S△BOD= S△ABF.
问题拓展:
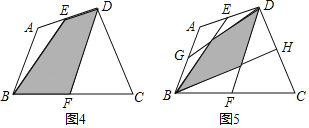
(4)①如图4,E、F分别为四边形ABCD的边AD、BC的中点,请直接写出阴影部分的面积与四边形ABCD的面积之间的数量关系:S阴影= S四边形ABCD.
②如图5,E、F、G、H分别为四边形ABCD的边AD、BC、AB、CD的中点,请直接写出阴影部分的面积与四边形ABCD的面积之间的数量关系:S阴影= S四边形ABCD.
参考答案:
【答案】问题解决:![]() ;问题探究:(2)证明见解析;(3)
;问题探究:(2)证明见解析;(3)![]() ,
,![]() ,
,![]() ;问题拓展:(4)①
;问题拓展:(4)①![]() ;②
;②![]() .
.
【解析】
问题解决:根据中线的性质即可得出结论;
问题探究:(2)根据问题解决的结论可得,S△BCD=![]() S△ABC,S△BCE=
S△ABC,S△BCE=![]() S△ABC,然后根据等式的基本性质即可得出S△BOD=S△COE;
S△ABC,然后根据等式的基本性质即可得出S△BOD=S△COE;
(3)根据中线的性质和探究结论(1)(2)可推出S△AOE=S△AOD=S△BOF=S△COF=S△BOD=S△COE=![]() S△ABC,从而得出结论;
S△ABC,从而得出结论;
问题拓展:(4)①连接BD,根据中线的性质可得S△ABE=S△BDE和S△BDF=S△DFC,从而得出结论;②连接BD,设BE交DG于M,BH交DF于N,根据问题探究:(3)的结论,可得S△BDM=![]() S△ABD,S△BDN=
S△ABD,S△BDN=![]() S△BDC,,从而得出结论.
S△BDC,,从而得出结论.
解:问题解决:∵AF是BC边上的中线,
∴S△ABF=S△AFC,
∴S△ABF=![]() S△ABC,
S△ABC,
故答案为![]() .
.
问题探究:(2)△ABC中,由问题解决的结论可得,S△BCD=![]() S△ABC,S△BCE=
S△ABC,S△BCE=![]() S△ABC.
S△ABC.
∴S△BCD=S△BCE
∴S△BCD﹣S△BOC=S△BCE﹣S△BOC
∴S△BOD=S△COE.
(3)∵CD,BE,AF分别是△ABC的中线,
∴S△BOF=S△COF, S△BAF=S△CAF,S△BOD=S△AOD,
利用探究结论(1)(2)易证:S△BOC=S四边形ADOE, S△BOD=S△COE
∴S△AOD=S△BAF-S△BOD-S△BOF=S△CAF-S△COE-S△COF=S△AOE
∴S△BOC=2S△BOF,S四边形ADOE=2S△AOD
∴S△BOF=S△AOD
∴S△AOE=S△AOD=S△BOF=S△COF=S△BOD=S△COE=![]() S△ABC,
S△ABC,
S△BOC=2S△BOF=![]() S△ABC,S△AOE=
S△ABC,S△AOE=![]() S△ABC,S△BOD=
S△ABC,S△BOD=![]() S△ABF.
S△ABF.
故答案为![]() ,
,![]() ,
,![]() .
.
问题拓展:(4)①如图4中,连接BD.

∵BE是△ABD的中线,
∴S△ABE=S△BDE,
∵DF是△BCD的中线,
∴S△BDF=S△DFC,
∴S阴=![]() S四边形ABCD,
S四边形ABCD,
故答案为![]() .
.
②如图5中,连接BD,设BE交DG于M,BH交DF于N.
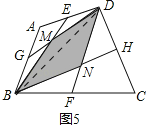
用问题探究可知:S△BDM=![]() S△ABD,S△BDN=
S△ABD,S△BDN=![]() S△BDC,
S△BDC,
∴S阴=![]() (S△ABD+S△BDC)=
(S△ABD+S△BDC)=![]() S四边形ABCD,
S四边形ABCD,
故答案为![]() .
.
-
科目: 来源: 题型:
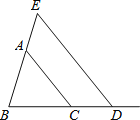
查看答案和解析>>【题目】如图,已知△ABC.
(1)若AB=4,AC=5,则BC边的取值范围是 ;
(2)点D为BC延长线上一点,过点D作DE∥AC,交BA的延长线于点E,若∠E=55°,∠ACD=125°,求∠B的度数.
-
科目: 来源: 题型:
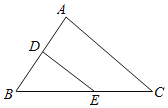
查看答案和解析>>【题目】如图,在△ABC中、D、E分别是AB,BC上任意一点,连结DE,若BD=4,DE=5.
(1)BE的取值范围 ;
(2)若DE∥AC,∠A=85°,∠BED=35°,求∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着新能源汽车推广力度加大,产业快速发展,越来越多的消费者接受并购买新能源汽车。我市某品牌新能源汽车经销商1月至3月份统计,该品牌汽车1月份销售150辆,3月份销售216辆.
(1)求该品牌新能源汽车销售量的月均增长率;
(2)若该品牌新能源汽车的进价为52000元,售价为58000元,则该经销商1月至3月份共盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图两个4×4网格都是由16个边长为1的小正方形组成.
(1)图①中的阴影正方形的顶点在网格的格点上,这个阴影正方形的面积为 ,若这个正方形的边长为
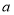 ,则
,则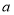 = ;
= ;(2)请在图②中画出面积是5的正方形,使它的顶点在网格的格点上.若这个正方形的边长为
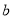 ,则
,则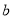 = ;
= ;(3)请你利用以上结论,在 图③ 的数轴上精确画出实数
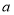 和-
和-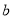 ,利用数轴可得
,利用数轴可得
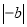 .(填“﹥”或“﹤
.(填“﹥”或“﹤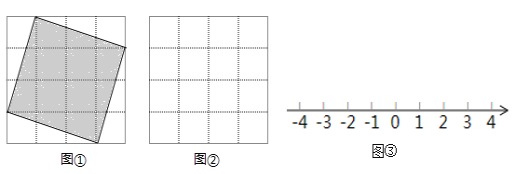
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形.请解答下列问题:
(1)写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称;
(2)探究:当等对角线四边形中两条对角线所夹锐角为60°时,这对60°角所对的两边之和与其中一条对角线的大小关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小完全相同,小明从布袋里随机取出一个小球,记下数字为x,小红在剩下的3个小球中随机取出一个小球,记下数字为y
(1)计算由x、y确定的点(x,y)在函数y=﹣x+5的图象上的概率.
(2)小明和小红约定做一个游戏,其规则为:若x、y满足xy>6,则小明胜;若x、y满足xy<6,则小红胜,这个游戏公平吗?请说明理由;若不公平,请写出公平的游戏规则.
相关试题

