【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC. 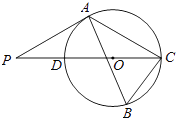
(1)求证:PA是⊙O的切线;
(2)若AB=4+ ![]() ,BC=2
,BC=2 ![]() ,求⊙O的半径.
,求⊙O的半径.
参考答案:
【答案】
(1)证明:连接OA,
∵∠B=60°,
∴∠AOC=2∠B=120°,
又∵OA=OC,
∴∠OAC=∠OCA=30°,
又∵AP=AC,
∴∠P=∠ACP=30°,
∴∠OAP=∠AOC﹣∠P=90°,
∴OA⊥PA,
∴PA是⊙O的切线
(2)解:过点C作CE⊥AB于点E.
在Rt△BCE中,∠B=60°,BC=2 ![]() ,
,
∴BE= ![]() BC=
BC= ![]() ,CE=3,
,CE=3,
∵AB=4+ ![]() ,
,
∴AE=AB﹣BE=4,
∴在Rt△ACE中,AC= ![]() =5,
=5,
∴AP=AC=5.
∴在Rt△PAO中,OA= ![]() ,
,
∴⊙O的半径为 ![]() .
.
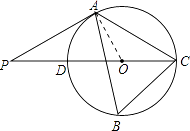
【解析】(1)连接OA,根据圆周角定理求出∠AOC,再由OA=OC得出∠ACO=∠OAC=30°,再由AP=AC得出∠P=30°,继而由∠OAP=∠AOC﹣∠P,可得出OA⊥PA,从而得出结论;(2)过点C作CE⊥AB于点E.在Rt△BCE中,∠B=60°,BC=2 ![]() ,于是得到BE=
,于是得到BE= ![]() BC=
BC= ![]() ,CE=3,根据勾股定理得到AC=
,CE=3,根据勾股定理得到AC= ![]() =5,于是得到AP=AC=5.解直角三角形即可得到结论.
=5,于是得到AP=AC=5.解直角三角形即可得到结论.
-
科目: 来源: 题型:
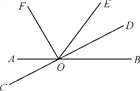
查看答案和解析>>【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线AB:y=5x﹣5与x轴交于点A,与y轴交于点B,点C与点B关于原点O对称,抛物线y=ax2+bx+c的对称轴为直线x=3且过点A和C.
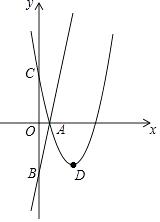
(1)求点A和点C的坐标;
(2)求抛物线y=ax2+bx+c的解析式;
(3)若抛物线y=ax2+bx+c的顶点为D,且在x轴上存在点P使得△DAP的面积为6,直接写出满足条件的点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两直线AB,CD相交于点O,已知OE平分∠BOD,且∠AOC:∠AOD=3:7,

(1)求∠DOE的度数;
(2)若OF⊥OE,求∠COF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校刚完成一批结构相同的学生宿舍的修建,这些宿舍地板需要铺瓷砖,一天4名一级技工去铺4个宿舍,结果还剩12 m2地面未铺瓷砖;同样时间内6名二级技工铺4个宿舍刚好完成,已知每名一级技工比二级技工一天多铺3 m2瓷砖.
(1)求每个宿舍需要铺瓷砖的地板面积.
(2)现该学校有20个宿舍的地板和36 m2的走廊需要铺瓷砖,某工程队有4名一级技工和6名二级技工,一开始有4名一级技工来铺瓷砖,3天后,学校根据实际情况要求2天后必须完成剩余的任务,所以决定加入一批二级技工一起工作,问需要再安排多少名二级技工才能按时完成任务
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,为美化校园环境,某校计划在一块长为100米,宽为60米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米﹒
(1)用含a的式子表示花圃的面积;
(2)如果通道所占面积是整个长方形空地面积的
 ,求出此时通道的宽;
,求出此时通道的宽;(3)已知某园林公司修建通道的单价是50元/米2,修建花圃的造价y(元)与花圃的修建面积S(m2)之间的函数关系如图2所示,并且通道宽a(米)的值能使关于x的方程
 x2-ax+25a-150有两个相等的实根,并要求修建的通道的宽度不少于5米且不超过12米,如果学校决定由该公司承建此项目,请求出修建的通道和花圃的造价和为多少元?
x2-ax+25a-150有两个相等的实根,并要求修建的通道的宽度不少于5米且不超过12米,如果学校决定由该公司承建此项目,请求出修建的通道和花圃的造价和为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是_____(填写符合要求的序号)
(1)两个有理数的和为负数时,这两个数都是负数;
(2)如果两个数的差是正数,那么这两个数都是正数;
(3)几个有理数相乘,当负因数个数为奇数时,乘积一定为负;
(4)数轴上到原点的距离为3的点表示的数是3或﹣3;
(5)0乘以任何数都是0.
相关试题

