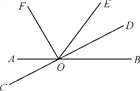
【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
参考答案:
【答案】(1) ∠COE,∠AOD,∠BOC;(2)∠AOD=149°,∠EOF=59°;(3) 射线OD与OF互相垂直,理由见解析.
【解析】试题分析:(1)根据互补的定义确定∠DOE的补角;
(2)先根据角平分线的定义得出∠BOD的度数,再由邻补角定义可得∠AOD=180°-∠BOD;之后根据邻补角定义可得∠AOE=180°-∠BOE,再由角平分线的定义得出∠EOF的度数;
(3)运用平角的定义和角平分线的定义,证明∠DOF是90°,得直线OD、OF的位置关系.
解:(1)∠DOE的补角为:∠COE,∠AOD,∠BOC.
(2)∵OD是∠BOE的平分线,∠BOE=62°,
∴∠BOD=![]() ∠BOE=31°.
∠BOE=31°.
∴∠AOD=180°-∠BOD=149°.
∴∠AOE=180°-∠BOE=118°.
又∵OF是∠AOE的平分线,
∴∠EOF=![]() ∠AOE=59°.
∠AOE=59°.
(3)射线OD与OF互相垂直.理由如下:
∵OF,OD分别是∠AOE,∠BOE的平分线,
∴∠DOF=∠DOE+∠EOF=![]() ∠BOE+
∠BOE+![]() ∠EOA=
∠EOA=![]() (∠BOE+∠EOA)=
(∠BOE+∠EOA)=![]() ×180°=90°.
×180°=90°.
∴OD⊥OF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点P(a+1,a-1)在x轴上,那么点P的坐标为( )
A. (-2,0) B. (2,0) C. (0,-2) D. (0,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)化简后再求值:
 ,其中
,其中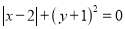
(2)若关于x、y的单项式cx2a+2y2与0.4xy3b+4的和为零,则
 a2b-[
a2b-[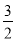 a2b-(3abc-a2c)-4a2c]-3abc的值又是多少?
a2b-(3abc-a2c)-4a2c]-3abc的值又是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】点A,B的坐标分别为(-2,3)和(1,3),抛物线y=ax2+bx+c(a<0)的 顶点在线段AB上运动时,形状保持不变,且与x轴交于C,D两点(C在D的左侧),给出下列结论:①c<3;②当x<-3时,y随x的增大而增大;③若点D的横坐标最大值为5,则点C的横坐标最小值为-5;④当四边形ACDB为平行四边形时,a=
 .其中正确的是( )
.其中正确的是( )A. ②④ B. ②③ C. ①③④ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出数轴上比6小的所有非负整数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于点E,点G是AE中点且∠AOG=30°,则下列结论正确的个数为( )
(1)DC=3OG; (2)OG= BC; ( 3)OGE是等边三角形; ( 4)SAOE=
BC; ( 3)OGE是等边三角形; ( 4)SAOE=  S矩形ABCD
S矩形ABCD
A. 1
B. 2
C. 3
D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
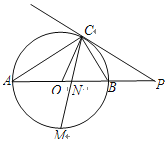
(1)求证:PC是⊙O的切线;
(2)求证:BC=
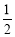 AB;
AB;(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN
 MC的值.
MC的值.
相关试题

