【题目】某学校刚完成一批结构相同的学生宿舍的修建,这些宿舍地板需要铺瓷砖,一天4名一级技工去铺4个宿舍,结果还剩12 m2地面未铺瓷砖;同样时间内6名二级技工铺4个宿舍刚好完成,已知每名一级技工比二级技工一天多铺3 m2瓷砖.
(1)求每个宿舍需要铺瓷砖的地板面积.
(2)现该学校有20个宿舍的地板和36 m2的走廊需要铺瓷砖,某工程队有4名一级技工和6名二级技工,一开始有4名一级技工来铺瓷砖,3天后,学校根据实际情况要求2天后必须完成剩余的任务,所以决定加入一批二级技工一起工作,问需要再安排多少名二级技工才能按时完成任务
参考答案:
【答案】(1)每个宿舍需要铺瓷砖的地板面积为18 m2;(2)需要再安排4名二级技工才能按时完成任务.
【解析】
(1)设每个宿舍需要铺瓷砖的地板面积为xm2,根据每名一级技工比二级技工一天多铺3m2瓷砖列出方程,然后求解即可;
(2)设需要再安排y名二级技工才能按时完成任务,根据每名一级技工每天可铺砖面积和每名二级技工每天可铺砖面积列出方程,然后求解即可得出答案.
(1)设每个宿舍需要铺瓷砖的地板面积为x m2,则依题意列出方程:
![]() -
-![]() =3,
=3,
解方程得:x=18.
所以每个宿舍需要铺瓷砖的地板面积为18 m2.
(2)设需要再安排y名二级技工才能按时完成任务.
因为每名一级技工每天可铺砖面积:![]() =15(m2),
=15(m2),
每名二级技工每天可铺砖面积:15-3=12(m2),
所以15×4×5+2×12y=20×18+36.
解得:y=4.
所以需要再安排4名二级技工才能按时完成任务.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明袋子中装有颜色不同的黑、白两种球共40个球,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程.如图是“摸到白球”的频率折线统计图:
(1)根据统计图,估算盒子里黑、白两种颜色的球各多少个?
(2)如果要使摸到白球的概率为
 ,需要往盒子里再放入多少个白球?
,需要往盒子里再放入多少个白球?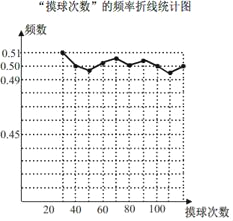
-
科目: 来源: 题型:
查看答案和解析>>【题目】某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,
 ≈1.7)
≈1.7)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.

(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=acm,其它条件不变,你能猜想MN的长度吗?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3).
(1)求抛物线的解析式;
(2)D是y轴正半轴上的点,OD=3,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,
①试说明EF是圆的直径;
②判断△AEF的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别交AB、AC于E、F两点,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是__________,△AEF的周长是__________;
(2)如图2,若将(1)中“△ABC中,AB=AC=10”该为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长;
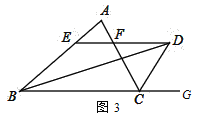
(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在∠AOB的内部作射线OC,使∠AOC与∠AOB互补.将射线OA,OC同时绕点O分别以每秒12°,每秒8°的速度按逆时针方向旋转,旋转后的射线OA,OC分别记为OM,ON,设旋转时间为t秒.已知t<30,∠AOB=114°.
(1)求∠AOC的度数;
(2)在旋转的过程中,当射线OM,ON重合时,求t的值;
(3)在旋转的过程中,当∠COM与∠BON互余时,求t的值.

相关试题

