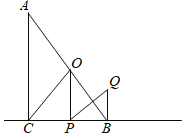
【题目】如图所示,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与B、C重合),连接OC、OP,将OP绕点P顺时针旋转60°,得到线段PQ,连接BQ,若∠BPO=15°,BP=4,则BQ的长为_____.
参考答案:
【答案】2+2![]() 或4
或4![]() ﹣4
﹣4
【解析】
分两种情况:①当点P在CB延长线上时,连接OQ,证得△OBC是等边三角形得出![]() ,由旋转的性质得出△OPQ是等边三角形,得出
,由旋转的性质得出△OPQ是等边三角形,得出![]() ,推出
,推出![]() ,由SAS证得
,由SAS证得![]() 得出
得出![]() ,证得
,证得![]() ,过点P作PD⊥BQ于D,则
,过点P作PD⊥BQ于D,则![]() ,由勾股定理得出
,由勾股定理得出![]() ,证得△QDP是等腰直角三角形得出
,证得△QDP是等腰直角三角形得出![]() ,则
,则![]() ;
;
②当点P在BC延长线上时,连接OQ,证得△OBC是等边三角形得出![]() ,推出
,推出![]() ,由旋转的性质得出△OPQ是等边三角形得出
,由旋转的性质得出△OPQ是等边三角形得出![]() ,推出
,推出![]() ,由SAS证得
,由SAS证得![]() 得出
得出![]() ,证得
,证得![]() ,过点Q作QE⊥BP于E,则
,过点Q作QE⊥BP于E,则![]() ,设
,设![]() ,则
,则![]() ,由勾股定理得出
,由勾股定理得出![]() ,由等腰直角三角形的性质得出
,由等腰直角三角形的性质得出![]() ,则
,则![]() ,求解即可得出答案.
,求解即可得出答案.
依题意,分以下两种情况:
①如图1,当点P在CB延长线上时,连接OQ
![]() 中,点O为AB中点
中,点O为AB中点
![]()
![]()
![]()
∴△OBC是等边三角形
![]()
∵OP绕点P顺时针旋转![]() ,得到线段PQ
,得到线段PQ
∴△OPQ是等边三角形
![]()
![]()
在△COP和△BOQ中,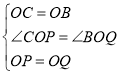
![]()
![]()
![]()
![]()
过点P作PD⊥BQ于D,则![]()
![]()
![]()
∴△QDP是等腰直角三角形
![]()
![]() ;
;
②如图2,当点P在BC延长线上时,连接OQ
![]() 中,点O为AB中点
中,点O为AB中点
![]()
![]()
![]()
∴△OBC是等边三角形
![]()
![]()
∵OP绕点P顺时针旋转![]() ,得到线段PQ
,得到线段PQ
∴△OPQ是等边三角形
![]()
![]()
在△COP和△BOQ中,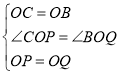
![]()
![]()
![]()
![]()
![]()
过点Q作QE⊥BP于E,则![]()
设![]() ,则
,则![]()
![]()
![]()
![]()
![]()
解得![]() ,即
,即![]()
综上,BQ的长为![]() 或
或![]()
故答案为:![]() 或
或![]() .
.

-
科目: 来源: 题型:
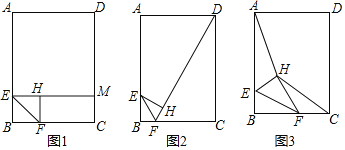
查看答案和解析>>【题目】如图,点E,F分别在矩形ABCD的边AB,BC上,连接EF,将△BEF沿直线EF翻折得到△HEF,AB=8,BC=6,AE:EB=3:1.
(1)如图1,当∠BEF=45°时,EH的延长线交DC于点M,求HM的长;
(2)如图2,当FH的延长线经过点D时,求tan∠FEH的值;
(3)如图3,连接AH,HC,当点F在线段BC上运动时,试探究四边形AHCD的面积是否存在最小值?若存在,求出四边形AHCD的面积的最小值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在
 中,
中, 以
以 的中点
的中点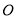 为圆心,作半圆与
为圆心,作半圆与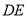 相切,点
相切,点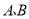 分别是半圆和边
分别是半圆和边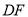 上的动点,连接
上的动点,连接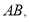 则
则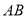 的最大值与最小值的和是( )
的最大值与最小值的和是( )
A.
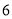 B.
B.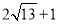 C.
C.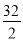 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中四边形OABC是边长为6的正方形,平行于对角线AC的直线l从O出发,沿x轴正方向以每秒一个单位长度的速度运动,运动到直线l与正方形没有交点为止,设直线l扫过正方形OABC的面积为S,直线l的运动时间为t(秒),下列能反映S与t之间的函数图象的是( )
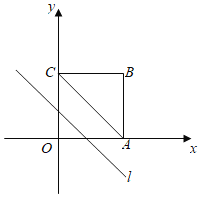
A.
 B.
B.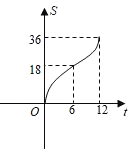
C.
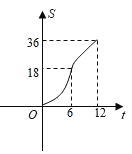 D.
D.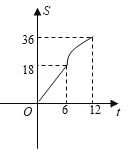
-
科目: 来源: 题型:
查看答案和解析>>【题目】焦作市教育局为调查全市教师的运动情况,结合现今流行的“微信运动”,随机调查了本市
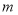 名老师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表:
名老师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表:步数
频数
频率
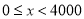
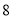
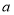
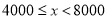
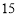
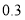
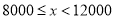
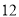
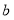
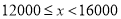
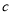
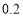
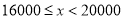
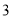
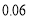
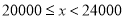
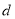
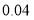
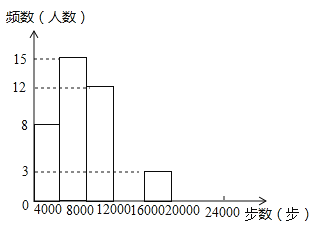
请根据以上信息,解答下列问题:
(1)写出
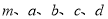 的值,并补全频数分布直方图;
的值,并补全频数分布直方图;(2)本市约有
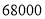 名教师,结合调查的数据估计日行走步数超过
名教师,结合调查的数据估计日行走步数超过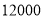 步(包含
步(包含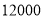 步)的教师有多少名?
步)的教师有多少名?(3)若在被调查的教师中,选取日行走步数超过
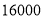 步(包含
步(包含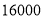 步)的两名教师与大家分享心得,求被选取的两名教师恰好都在
步)的两名教师与大家分享心得,求被选取的两名教师恰好都在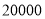 步(包含
步(包含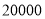 步)以上的概率.
步)以上的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】河南省政府为促进农业发展,加快农村建设,计划扶持兴建一批新型钢管装配式大棚,如图1所示线段AB、BD分别为大棚的墙高和跨度,AC表示保温板的长,已知墙高AB为3米,墙面与保温板所成的角∠BAC=150°,在点D处测得A点、C点的仰角分别为9°,15.6°,如图2所示求保温板AC的长是多少米?(精确到0.1米)(参考数据:sin9°≈0.16,cos9°≈0.99,tan9°≈0.16,sin15.6°≈0.27,cos15.6°≈0.96,tan15.6°≈0.28,
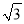 ≈1.73)
≈1.73)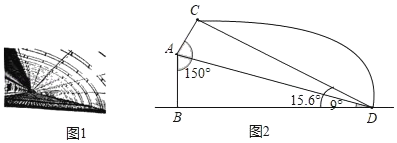
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点M、N分别是x轴y轴上的动点,点P、Q是某个函数图象上的点,当四边形MNPQ为正方形时,称这个正方形为此函数的“梦幻正方形”例如:如图1所示,正方形MNPQ是一次函数y=﹣x+2的其中一个“梦幻正方形”.
(1)若某函数是y=x+5,求它的图象的所有“梦幻正方形”的边长;
(2)若某函数是反比例函数y=
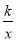 (k<0)(如图2所示),它的图象的“梦幻正方形”ABCD,D(﹣4,m)(m<4)在反比例函数图象上,求m的值及反比例函数的解析式.
(k<0)(如图2所示),它的图象的“梦幻正方形”ABCD,D(﹣4,m)(m<4)在反比例函数图象上,求m的值及反比例函数的解析式.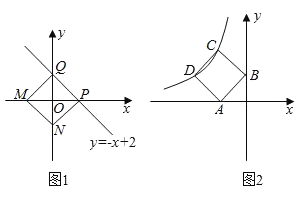
相关试题

