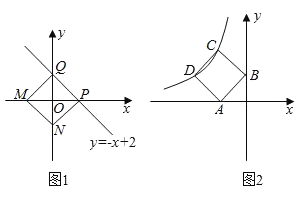
【题目】已知:点M、N分别是x轴y轴上的动点,点P、Q是某个函数图象上的点,当四边形MNPQ为正方形时,称这个正方形为此函数的“梦幻正方形”例如:如图1所示,正方形MNPQ是一次函数y=﹣x+2的其中一个“梦幻正方形”.
(1)若某函数是y=x+5,求它的图象的所有“梦幻正方形”的边长;
(2)若某函数是反比例函数y=![]() (k<0)(如图2所示),它的图象的“梦幻正方形”ABCD,D(﹣4,m)(m<4)在反比例函数图象上,求m的值及反比例函数的解析式.
(k<0)(如图2所示),它的图象的“梦幻正方形”ABCD,D(﹣4,m)(m<4)在反比例函数图象上,求m的值及反比例函数的解析式.
参考答案:
【答案】(1)一次函数y=x+5图象的“梦幻正方形”的边长为5![]() 或
或![]() ;(2)m=2.反比例函数的解析式为y=﹣
;(2)m=2.反比例函数的解析式为y=﹣![]()
【解析】
(1)先正确地画出图形,再利用正方形的性质确定相关点的坐标从而计算正方形的边长;
(2)因为ABCD为正方形,所以可作垂线得到等腰直角三角形,利用点![]() 的坐标表示出点C的坐标,再利用待定系数法得到一个关于m、k方程组,然后求解即可.
的坐标表示出点C的坐标,再利用待定系数法得到一个关于m、k方程组,然后求解即可.
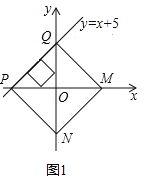
(1)如图1,当点M在x轴正半轴,点N在y轴负半轴上时
![]()
∴正方形MNPQ的边长![]()
设小正方形的边长为a
则![]()
解得![]() ,即小正方形边长为
,即小正方形边长为![]()
故一次函数![]() 图象的“梦幻正方形”的边长为
图象的“梦幻正方形”的边长为![]() 或
或![]() ;
;
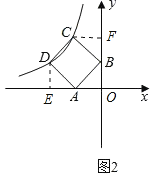
(2)如图2,作DE,CF分别垂直于x、y轴
易知![]()
![]()
![]()
![]()
![]()
∴C点坐标为![]()
将点C、D坐标代入反比例函数的解析式得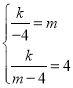
解得![]()
故反比例函数的解析式为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与B、C重合),连接OC、OP,将OP绕点P顺时针旋转60°,得到线段PQ,连接BQ,若∠BPO=15°,BP=4,则BQ的长为_____.
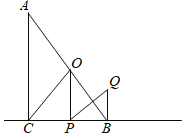
-
科目: 来源: 题型:
查看答案和解析>>【题目】焦作市教育局为调查全市教师的运动情况,结合现今流行的“微信运动”,随机调查了本市
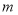 名老师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表:
名老师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表:步数
频数
频率
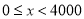
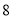
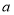
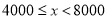
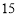
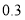
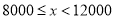
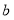
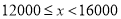
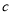
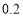
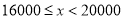
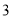
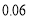
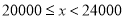
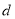
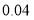
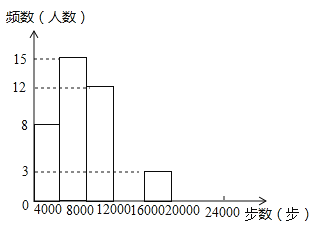
请根据以上信息,解答下列问题:
(1)写出
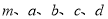 的值,并补全频数分布直方图;
的值,并补全频数分布直方图;(2)本市约有
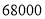 名教师,结合调查的数据估计日行走步数超过
名教师,结合调查的数据估计日行走步数超过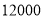 步(包含
步(包含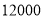 步)的教师有多少名?
步)的教师有多少名?(3)若在被调查的教师中,选取日行走步数超过
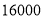 步(包含
步(包含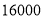 步)的两名教师与大家分享心得,求被选取的两名教师恰好都在
步)的两名教师与大家分享心得,求被选取的两名教师恰好都在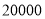 步(包含
步(包含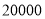 步)以上的概率.
步)以上的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】河南省政府为促进农业发展,加快农村建设,计划扶持兴建一批新型钢管装配式大棚,如图1所示线段AB、BD分别为大棚的墙高和跨度,AC表示保温板的长,已知墙高AB为3米,墙面与保温板所成的角∠BAC=150°,在点D处测得A点、C点的仰角分别为9°,15.6°,如图2所示求保温板AC的长是多少米?(精确到0.1米)(参考数据:sin9°≈0.16,cos9°≈0.99,tan9°≈0.16,sin15.6°≈0.27,cos15.6°≈0.96,tan15.6°≈0.28,
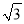 ≈1.73)
≈1.73)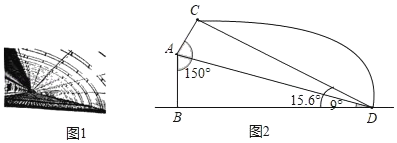
-
科目: 来源: 题型:
查看答案和解析>>【题目】春节前夕,某批发部从厂家购进A、B两种礼盒,已知购进2个A礼盒和3个B礼盒共花520元;购进3个A礼盒和2个B礼盒共花费480元.
(1)求A、B两种礼盒的单价分别是多少元?
(2)该批发部经理购进这两种礼盒恰好用去4800元购进A种礼盒最多18个,B种礼盒的数量不超过A种礼盒数量的2倍,共有几种进货方案?
(3)已知销售一个A种礼盒可获利10元,销售一个B种礼盒可获利18元,该店主决定每售出一个B种礼盒,为爱心公益基金捐款m元,每个A种礼盒的利润不变,在(2)的条件下,要使A、B两种礼盒全部售出后所有方案获利均相同,m的值应是多少?此时这个批发部获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方形
 中,
中,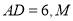 在
在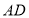 上从
上从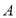 向
向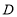 运动,连接
运动,连接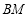 交
交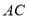 于
于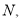 连接
连接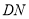 .
.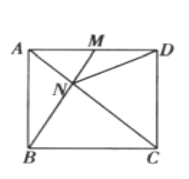
(1)证明:无论
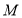 运动到
运动到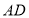 上的何处,都有
上的何处,都有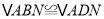 ;
;(2)当
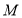 运动到何处时,
运动到何处时,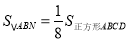 ?
?(3)若
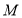 从
从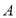 到
到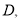 再从
再从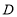 到
到 ,在整个运动过程中,
,在整个运动过程中,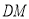 为多少时,
为多少时,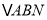 是等腰三角形?
是等腰三角形? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,抛物线y=ax2+bx+c与x轴交于A、B两点,A(﹣5,0),与y轴交于C(0,﹣5),并且对称轴x=﹣3.
(1)求抛物线的解析式;
(2)P在x轴上方的抛物线上,过P的直线y=x+m与直线AC交于点M,与y轴交于点N,求PM+MN的最大值;
(3)点D为抛物线对称轴上一点,
①当△ACD是以AC为直角边的直角三角形时,求D点坐标;
②若△ACD是锐角三角形,求点D的纵坐标的取值范围.
相关试题

