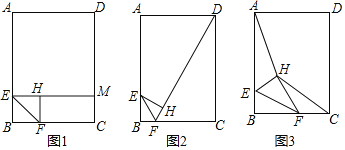
【题目】如图,点E,F分别在矩形ABCD的边AB,BC上,连接EF,将△BEF沿直线EF翻折得到△HEF,AB=8,BC=6,AE:EB=3:1.
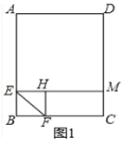
(1)如图1,当∠BEF=45°时,EH的延长线交DC于点M,求HM的长;
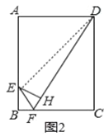
(2)如图2,当FH的延长线经过点D时,求tan∠FEH的值;
(3)如图3,连接AH,HC,当点F在线段BC上运动时,试探究四边形AHCD的面积是否存在最小值?若存在,求出四边形AHCD的面积的最小值;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,四边形
;(3)存在,四边形![]() 的面积的最小值为
的面积的最小值为![]() .
.
【解析】
(1)当∠BEF=45°时,易知四边形EBFH是正方形,求出EM,EH的长即可解决问题.
(2)如图2中,连接DE.利用勾股定理求出DE,DH,设BF=FH=x,在Rt△DFC中,利用勾股定理即可解决问题.
(3)如图3中,连接AC,作EM⊥AC于M.利用相似三角形的性质求出EM,由S四边形AHCD=S△ACH+S△ADC,S△ACD=![]() ×6×8=24,推出当△ACH的面积最小时,四边形AHCD的面积最小,可知当EH与EM重合时,点H到直线AC的距离最小,由此即可解决问题.
×6×8=24,推出当△ACH的面积最小时,四边形AHCD的面积最小,可知当EH与EM重合时,点H到直线AC的距离最小,由此即可解决问题.
(1)如图1中,
当![]() 时,易知四边形
时,易知四边形![]() 是正方形,
是正方形,
∵![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
![]() ,
,
![]() .
.
(2)如图2中,连接![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
在![]() 中,
中,![]()
设![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(3)如图3中,连接![]() ,作
,作![]() 于
于![]() .
.

![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 当
当![]() 的面积最小时,四边形
的面积最小时,四边形![]() 的面积最小,
的面积最小,
![]() 当
当![]() 与
与![]() 重合时,点
重合时,点![]() 到直线
到直线![]() 的距离最小,最小值
的距离最小,最小值![]() ,
,
![]() 的面积的最小值
的面积的最小值![]() ,
,
![]() 四边形
四边形![]() 的面积的最小值为
的面积的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x
…
﹣3
﹣2
﹣1
0
1
2
3
…
y
…
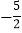
﹣4
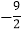
﹣4
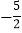
0

…
(1)求该抛物线的表达式;
(2)已知点E(4, y)是该抛物线上的点,点E关于抛物线的对称轴对称的点为点F,求点E和点F的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】世界500强H公司决定购买某演唱会门票奖励部分优秀员工,演唱会的购票方式有以下两种,
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元(其中总费用=广告赞助费+门票费);
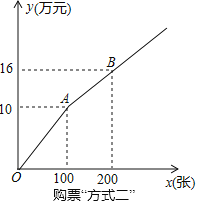
方式二:如图所示,设购买门票x张,总费用为y万元
(1)求用购票“方式一”时y与x的函数关系式;
(2)若H、A两家公司分别釆用方式一、方式二购买本场演唱会门票共400张,且A公司购买超过100张,两公司共花费27.2万元,求H、A两公司各购买门票多少张?
-
科目: 来源: 题型:
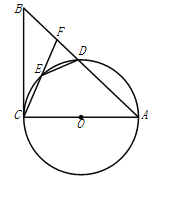
查看答案和解析>>【题目】如图,在⊿
 中,以
中,以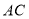 为直径的⊙
为直径的⊙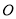 与边
与边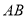 交于点
交于点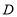 ,点
,点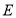 为⊙
为⊙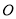 上一点,连接
上一点,连接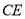 并延长交
并延长交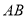 于点
于点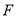 ,连接
,连接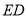 .
.
(1)若
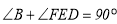 ;求证:
;求证: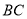 是⊙
是⊙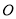 的切线;
的切线;(2)若
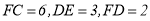 .求⊙
.求⊙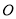 的直径.
的直径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在
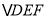 中,
中,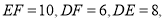 以
以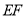 的中点
的中点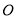 为圆心,作半圆与
为圆心,作半圆与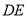 相切,点
相切,点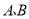 分别是半圆和边
分别是半圆和边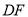 上的动点,连接
上的动点,连接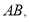 则
则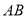 的最大值与最小值的和是( )
的最大值与最小值的和是( )
A.
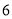 B.
B.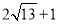 C.
C.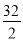 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中四边形OABC是边长为6的正方形,平行于对角线AC的直线l从O出发,沿x轴正方向以每秒一个单位长度的速度运动,运动到直线l与正方形没有交点为止,设直线l扫过正方形OABC的面积为S,直线l的运动时间为t(秒),下列能反映S与t之间的函数图象的是( )
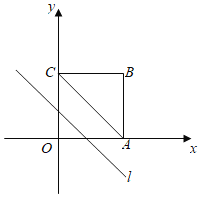
A.
 B.
B.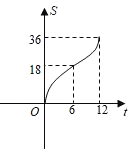
C.
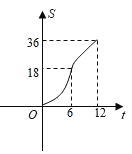 D.
D.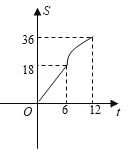
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与B、C重合),连接OC、OP,将OP绕点P顺时针旋转60°,得到线段PQ,连接BQ,若∠BPO=15°,BP=4,则BQ的长为_____.
相关试题

