【题目】已知直线![]() ,直线
,直线![]() 与直线
与直线![]() 、
、![]() 分别相交于C、D两点.
分别相交于C、D两点.
(1)如图a,有一动点P在线段CD之间运动(不与C、D两点重合),问在点P的运动过程中,是否始终具有∠3+∠1=∠2这一关系,为什么?
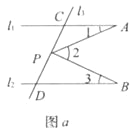
(2)如图b,当动点P线段CD之外运动(不与C、D两点重合),问上述结论是否成立?若不成立,试写出新的结论并说明理由.
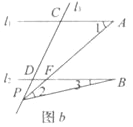
参考答案:
【答案】(1)具有,证明见解析;(2)上述结论不成立, 新结论:∠1=∠2+∠3,理由见解析.
【解析】试题分析:(1)相等关系成立.过点P作PE∥l1,则有∠1=∠APE,又因为PE∥l2,又有∠3=∠BPE,因为∠BPE+∠APE=∠2,所以∠3+∠1=∠2;
(2)原关系不成立,过点P作PE∥l1,则有∠1=∠APE;又因为PE∥l2,又有∠3=∠BPE,困为此时∠BPE-∠APE=∠2,则有∠3-∠1=∠2.
试题解析:
(1)作PE∥l1,则∠1=∠APE
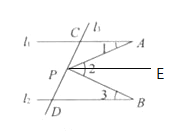
∵l1//l2,
∴l2//PE
∴∠3=∠BPE∵∠APB=∠APE+∠BPE
∴∠APB=∠1+∠3
(2)上述结论不成立. 新结论:∠1=∠2+∠3
∵l1//l2,
∴∠1=∠AFB
∵∠AFB=∠2+∠3
∴∠1=∠2+∠3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E,

(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论: ①∠BOE=
 (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.
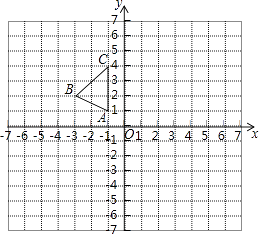
①画出与△ABC关于y轴对称的△A1B1C1 , 求点C1的坐标。
②以原点O为位似中心,在第四象限画一个△A2B2C2 , 使它与△ABC位似,并且△A2B2C2与△ABC的相似比为2:1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE
(1)判断OF与OD的位置关系,并进行证明.
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.

-
科目: 来源: 题型:
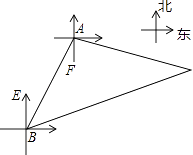
查看答案和解析>>【题目】如图,我东海舰队的一艘军舰在海面A处巡逻时发现一艘不明国籍的船只在C处游弋,立即通知在B处的另一艘军舰一起向其包抄,此时B在A的南偏西30°方向,我两艘军舰分别测得C在A的南偏东75°方向和C在B的北偏东75°方向,已知A,B之间的距离是30海里,求此刻我两艘军舰所在地A,B与C的距离.(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数
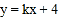 的图象经过点(-3,-2).
的图象经过点(-3,-2).(1)求这个函数表达式;
(2)判断(-5,3)是否在这个函数的图象上.
(3)点M在直线y=kx+4上且到y轴的距离是3,求点M的坐标.
相关试题

