【题目】以坐标原点为圆心,1为半径的圆分别交x,y轴的正半轴于点A,B.
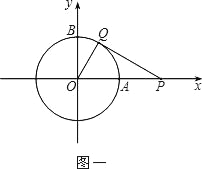
(1)如图一,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时PQ恰好是⊙O的切线,连接OQ.求∠QOP的大小;
(2)若点Q按照(1)中的方向和速度继续运动,点P停留在点(2,0)处不动,求点Q再经过5秒后直线PQ被⊙O截得的弦长.
参考答案:
【答案】(1)∠QOP=60°;(2)QD=![]() .
.
【解析】(1)解:如图一,连结AQ.
由题意可知:OQ=OA=1.
∵OP=2,
∴A为OP的中点.
∵PQ与![]() 相切于点Q,
相切于点Q,
∴![]() 为直角三角形.
为直角三角形.
∴![]() .
.
即ΔOAQ为等边三角形.
∴∠QOP=60°.
(2)解:由(1)可知点Q运动1秒时经过的弧长所对的圆心角为30°,若Q按照(1)中的方向和速度
继续运动,那么再过5秒,则Q点落在![]() 与y轴负半轴的交点处(如图二).
与y轴负半轴的交点处(如图二).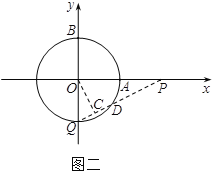
设直线PQ与![]() 的另外一个交点为D,过O作OC⊥QD于点C,则C为QD的中点.
的另外一个交点为D,过O作OC⊥QD于点C,则C为QD的中点.
∵∠QOP=90°,OQ=1,OP=2,
∴QP=![]() .
.
∵![]() ,
,
∴OC=![]() .
.
∵OC⊥QD,OQ=1,OC=![]() ,
,
∴QC=![]() .
.
∴QD=![]() .
.
(1)利用切线性质定理,以及OQ与OP之间的关系,可得出∠QOP的度数
(2)关键是求出Q点的运动速度,利用垂径定理,勾股定理可以解决.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了丰富学生课余生活,某区教育部分准备在七年级开设兴趣课堂,为了了解学生对音乐、书法、球类、绘画这四个兴趣小组的喜爱情况,在全区进行随机抽样调查,并根据收集的数据绘制了下面两幅统计图(信息不完整),请根据图中提供的信息,解答下面的问题:
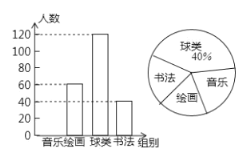
(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中音乐部分的圆心角的度数;
(3)如果该区七年级共有2000名学生参加这4个课外兴趣小组,则参加绘画兴趣小组的学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,三角形ABC三个顶点的坐标分别为
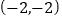 、
、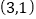 ,
,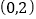 ,若把三角形ABC向上平移3个单位长度,再向左平移1个单位长度得到三角形A′B′C′,点A、B、C的对应点分别为A′、B′、C′。
,若把三角形ABC向上平移3个单位长度,再向左平移1个单位长度得到三角形A′B′C′,点A、B、C的对应点分别为A′、B′、C′。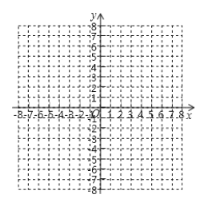
(1)写出点A′、B′、C′的坐标;
(2)在图中画出平移后的三角形A′B′C′;
(3)三角形A′B′C′的面积为_____________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:

(1)药物燃烧时,y关于x的函数关系式为________,自变量x的取值范为________;药物燃烧后,y关于x的函数关系式为________.
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过________分钟后,员工才能回到办公室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形
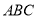 中,
中,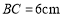 .射线
.射线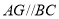 ,点
,点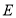 从点
从点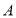 出发沿射线
出发沿射线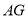 以
以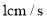 的速度运动,同点
的速度运动,同点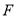 从点
从点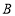 出发沿射线
出发沿射线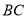 以
以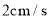 的速度运动,设运动时间为
的速度运动,设运动时间为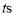 ;
;
(1)连接
 ,当
,当 经过
经过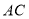 边的中点
边的中点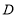 时,求证:
时,求证: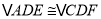 ;
;(2)求当
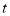 为何值,四边形
为何值,四边形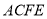 是平行四边形.
是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明:
已知:如图,点D、E、F分别在线段AB、BC、AC上,连接DE、EF、DM平分∠ADE交EF于点M,
 ,求证:
,求证: 。
。
证明:
 (已知)
(已知)又
 (平角定义)
(平角定义)∴∠2=∠BEM(____________________)
∴
 __________(_________________________)
__________(_________________________) (_____________________________)
(_____________________________) (_____________________________)
(_____________________________)又∵DM平分∠ADE(已知)
 (角平分线定义)
(角平分线定义)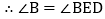 (等量代换)
(等量代换)
相关试题

