【题目】如图,等边△ABC边长为10,P在AB上,Q在BC延长线,CQ=PA,过点P作PE⊥AC点E,过点P作PF∥BQ,交AC边于点F,连接PQ交AC于点D,则DE的长为_____.

参考答案:
【答案】5
【解析】
先证明△PFD和△QCD全等,推出FD=CD,再通过证明△APF是等边三角形和PE⊥AC,推出AE=EF,即可推出AE+DC=EF+FD,可得DE=![]() AC,即可推出DE的长度.
AC,即可推出DE的长度.
∵PF∥BQ,
∴∠Q=∠FPD,
∵△ABC是等边三角形,
∴∠APF=∠B=60°,∠AFP=∠ACB=60°,
∴△APF是等边三角形,
∴AP=PF,
∵AP=CQ,
∴PF=CQ,
∵在△PFD和△QCD中,
 ,
,
∴△PFD≌△QCD(AAS),
∴FD=CD,
∵PE⊥AC于E,△APF是等边三角形,
∴AE=EF,
∴AE+DC=EF+FD,
∴DE=![]() AC,
AC,
∵AC=10,
∴DE=![]() AC=5.
AC=5.
故答案为:5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),且∠1=∠4( )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠ =∠3( )
又∵∠B=∠C(已知),∴∠3=∠B(等量代换)
∴AB∥CD ( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,直线y=﹣x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.

(1)求该抛物线的解析式;
(2)在该抛物线的对称轴上是否存在点M,使以C,P,M为顶点的三角形为等腰三角形?若存在,请直接写出所符合条件的点M的坐标;若不存在,请说明理由;
(3)当0<x<3时,在抛物线上求一点E,使△CBE的面积有最大值(图乙、丙供画图探究). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(﹣1,1)、B(4,6)在抛物线y=ax2+bx上
(1)求抛物线的解析式;
(2)如图1,点F的坐标为(0,m)(m>2),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H.设抛物线与x轴的正半轴交于点E,连接FH、AE,求证:FH∥AE;
(3)如图2,直线AB分别交x轴、y轴于C、D两点.点P从点C出发,沿射线CD方向匀速运动,速度为每秒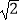
个单位长度;同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度.点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=2PM,直接写出t的值.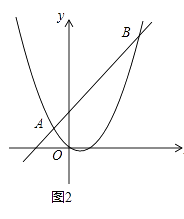
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形的顶点A,C分别在y轴和x轴上,边BC的中点F在y轴上,若反比例函数y=
 的图象恰好经过CD的中点E,则OA的长为______.
的图象恰好经过CD的中点E,则OA的长为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)2﹣2+(
 )0+(﹣0.2)2014×52014
)0+(﹣0.2)2014×52014(2)(2a3b)3(﹣8ab2)÷(﹣4a4b3)
(3)(2a+1)2﹣(2a+1)(﹣1+2a)
(4)20192﹣2018×2020(运用整式乘法公式进行计算)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.

(1)求抛物线的函数表达式;
(2)若点D是y轴上的一点,且以B,C,D为顶点的三角形与△ABC相似,求点D的坐标;
(3)如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标及最大面积;
(4)若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标.
相关试题

