【题目】已知点A(﹣1,1)、B(4,6)在抛物线y=ax2+bx上
(1)求抛物线的解析式;
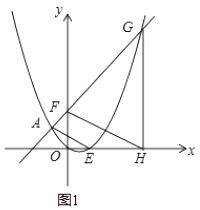
(2)如图1,点F的坐标为(0,m)(m>2),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H.设抛物线与x轴的正半轴交于点E,连接FH、AE,求证:FH∥AE;
(3)如图2,直线AB分别交x轴、y轴于C、D两点.点P从点C出发,沿射线CD方向匀速运动,速度为每秒 ![]()
个单位长度;同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度.点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=2PM,直接写出t的值.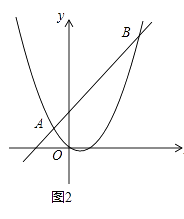
参考答案:
【答案】
(1)解:将点A(﹣1,1)、B(4,6)代入y=ax2+bx中,
![]() ,解得:
,解得:  ,
,
∴抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x.
x.
(2)证明:设直线AF的解析式为y=kx+m,
将点A(﹣1,1)代入y=kx+m中,即﹣k+m=1,
∴k=m﹣1,
∴直线AF的解析式为y=(m﹣1)x+m.
联立直线AF和抛物线解析式成方程组,
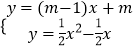 ,解得:
,解得: ![]() ,
, ![]() ,
,
∴点G的坐标为(2m,2m2﹣m).
∵GH⊥x轴,
∴点H的坐标为(2m,0).
∵抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x=
x= ![]() x(x﹣1),
x(x﹣1),
∴点E的坐标为(1,0).
设直线AE的解析式为y=k1x+b1,
将A(﹣1,1)、E(1,0)代入y=k1x+b1中,
![]() ,解得:
,解得: 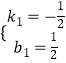 ,
,
∴直线AE的解析式为y=﹣ ![]() x+
x+ ![]() .
.
设直线FH的解析式为y=k2x+b2,
将F(0,m)、H(2m,0)代入y=k2x+b2中,
![]() ,解得:
,解得: 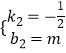 ,
,
∴直线FH的解析式为y=﹣ ![]() x+m.
x+m.
∴FH∥AE.
(3)设直线AB的解析式为y=k0x+b0,
将A(﹣1,1)、B(4,6)代入y=k0x+b0中,
![]() ,解得:
,解得: ![]() ,
,
∴直线AB的解析式为y=x+2.
当运动时间为t秒时,点P的坐标为(t﹣2,t),点Q的坐标为(t,0).
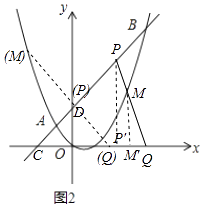
当点M在线段PQ上时,过点P作PP′⊥x轴于点P′,过点M作MM′⊥x轴于点M′,则△PQP′∽△MQM′,如图2所示.
∵QM=2PM,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴QM′= ![]() ,MM′=
,MM′= ![]() t,
t,
∴点M的坐标为(t﹣ ![]() ,
, ![]() t).
t).
又∵点M在抛物线y= ![]() x2﹣
x2﹣ ![]() x上,
x上,
∴ ![]() t=
t= ![]() ×(t﹣
×(t﹣ ![]() )2﹣
)2﹣ ![]() (t﹣
(t﹣ ![]() ),
),
解得:t= ![]() ;
;
当点M在线段QP的延长线上时,
同理可得出点M的坐标为(t﹣4,2t),
∵点M在抛物线y= ![]() x2﹣
x2﹣ ![]() x上,
x上,
∴2t= ![]() ×(t﹣4)2﹣
×(t﹣4)2﹣ ![]() (t﹣4),
(t﹣4),
解得:t= ![]() .
.
综上所述:当运动时间为 ![]() 秒、
秒、 ![]() 秒、
秒、 ![]() 秒或
秒或 ![]() 秒时,QM=2PM.
秒时,QM=2PM.
【解析】(1)利用待定系数法把A、B坐标代入解析式即可;(2)要证坐标系中的两直线平行,可求两直线的解析式,斜率k相等,两直线平行,常数b可不必求出;(3)须动手画出点M与线段PQ的两种相对位置,分类讨论,斜线段QM与PM的比,通过作垂线,转化为x轴上水平线段的比,构建方程,求出t.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从甲地到乙地有
 三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:公交车用时的频数
公交车用时线路




合计

59
151
166
124
500

50
50
122
278
500

45
265
160
30
500
早高峰期间,乘坐_________(填“
 ”,“
”,“ ”或“
”或“ ”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大. -
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),且∠1=∠4( )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠ =∠3( )
又∵∠B=∠C(已知),∴∠3=∠B(等量代换)
∴AB∥CD ( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,直线y=﹣x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.

(1)求该抛物线的解析式;
(2)在该抛物线的对称轴上是否存在点M,使以C,P,M为顶点的三角形为等腰三角形?若存在,请直接写出所符合条件的点M的坐标;若不存在,请说明理由;
(3)当0<x<3时,在抛物线上求一点E,使△CBE的面积有最大值(图乙、丙供画图探究). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC边长为10,P在AB上,Q在BC延长线,CQ=PA,过点P作PE⊥AC点E,过点P作PF∥BQ,交AC边于点F,连接PQ交AC于点D,则DE的长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形的顶点A,C分别在y轴和x轴上,边BC的中点F在y轴上,若反比例函数y=
 的图象恰好经过CD的中点E,则OA的长为______.
的图象恰好经过CD的中点E,则OA的长为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)2﹣2+(
 )0+(﹣0.2)2014×52014
)0+(﹣0.2)2014×52014(2)(2a3b)3(﹣8ab2)÷(﹣4a4b3)
(3)(2a+1)2﹣(2a+1)(﹣1+2a)
(4)20192﹣2018×2020(运用整式乘法公式进行计算)
相关试题

