【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( ) 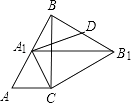
A.![]()
B.2 ![]()
C.3
D.2 ![]()
参考答案:
【答案】A
【解析】解:∵∠ACB=90°,∠ABC=30°,AC=2, ∴∠A=90°﹣∠ABC=60°,AB=4,BC=2 ![]() ,
,
∵CA=CA1 ,
∴△ACA1是等边三角形,AA1=AC=BA1=2,
∴∠BCB1=∠ACA1=60°,
∵CB=CB1 ,
∴△BCB1是等边三角形,
∴BB1=2 ![]() ,BA1=2,∠A1BB1=90°,
,BA1=2,∠A1BB1=90°,
∴BD=DB1= ![]() ,
,
∴A1D= ![]() =
= ![]() .
.
故选A.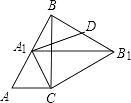
首先证明△ACA1 , △BCB1是等边三角形,推出△A1BD是直角三角形即可解决问题.
-
科目: 来源: 题型:
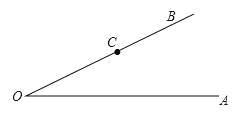
查看答案和解析>>【题目】如图:点C是∠AOB的边OB上的一点,按下列要求画图并回答问题.
(1)过C点画OB的垂线,交OA于点D;
(2)过C点画OA的垂线,垂足为E;
(3)比较线段CE,OD,CD的大小(请直接写出结论);
(4)请写出第(3)小题图中与∠AOB互余的角(不增添其它字母).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( )
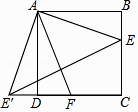
A.△AEE′是等腰直角三角形
B.AF垂直平分EE'
C.△E′EC∽△AFD
D.△AE′F是等腰三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明从点A出发,前进10m后向右转20°,再前进10m后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.
(1)小明一共走了多少米?
(2)这个多边形的内角和是多少度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.

(1)求证:△ABE≌△DAF;
(2)若AF=1,四边形ABED的面积为6,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的运算程序中,若开始输入的
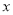 值为5,可发现第一次输出的结果为8,第二次输出的结果为4,…,请你探索第2020次输出的结果为( )
值为5,可发现第一次输出的结果为8,第二次输出的结果为4,…,请你探索第2020次输出的结果为( )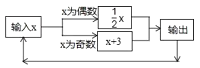
A.2B.1C.6D.4
-
科目: 来源: 题型:
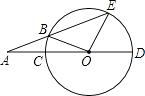
查看答案和解析>>【题目】如图,CD是⊙O的直径,∠EOD=72°,AE交⊙O于点B,且AB=OC,求∠A的度数.
相关试题

