【题目】如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( ) 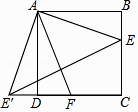
A.△AEE′是等腰直角三角形
B.AF垂直平分EE'
C.△E′EC∽△AFD
D.△AE′F是等腰三角形
参考答案:
【答案】D
【解析】解:∵将△ABE绕点A顺时针旋转90°,使点E落在点E'处, ∴AE′=AE,∠E′AE=90°,
∴△AEE′是等腰直角三角形,故A正确;
∵将△ABE绕点A顺时针旋转90°,使点E落在点E'处,
∴∠E′AD=∠BAE,
∵四边形ABCD是正方形,
∴∠DAB=90°,
∵∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠E′AD+∠FAD=45°,
∴∠E′AF=∠EAF,
∵AE′=AE,
∴AF垂直平分EE',故B正确;
∵AF⊥E′E,∠ADF=90°,
∴∠FE′E+∠AFD=∠AFD+∠DAF,
∴∠FE′E=∠DAF,
∴△E′EC∽△AFD,故C正确;
∵AD⊥E′F,但∠E′AD不一定等于∠DAE′,
∴△AE′F不一定是等腰三角形,故D错误;
故选D.
【考点精析】认真审题,首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°),还要掌握线段垂直平分线的性质(垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等)的相关知识才是答题的关键.
-
科目: 来源: 题型:
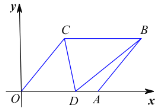
查看答案和解析>>【题目】如图,在平面直角坐标系
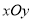 中,已知
中,已知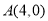 ,将线段
,将线段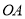 平移至
平移至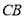 ,点
,点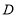 在
在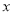 轴正半轴上,
轴正半轴上,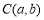 ,且
,且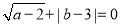 .连接
.连接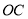 ,
,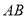 ,
,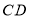 ,
,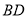 .
.
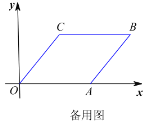
(1)写出点
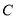 的坐标为 ;点
的坐标为 ;点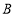 的坐标为 ;
的坐标为 ;(2)当
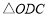 的面积是
的面积是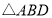 的面积的3倍时,求点
的面积的3倍时,求点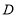 的坐标;
的坐标;(3)设
 ,
,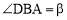 ,
,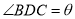 ,判断
,判断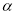 、
、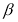 、
、 之间的数量关系,并说明理由.
之间的数量关系,并说明理由. -
科目: 来源: 题型:
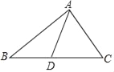
查看答案和解析>>【题目】如图所示,已知AD是△ABC的边BC上的中线.
(1)作出△ABD的边BD上的高;
(2)若△ABC的面积为10,求△ADC的面积;
-
科目: 来源: 题型:
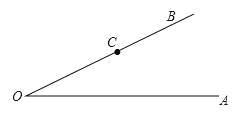
查看答案和解析>>【题目】如图:点C是∠AOB的边OB上的一点,按下列要求画图并回答问题.
(1)过C点画OB的垂线,交OA于点D;
(2)过C点画OA的垂线,垂足为E;
(3)比较线段CE,OD,CD的大小(请直接写出结论);
(4)请写出第(3)小题图中与∠AOB互余的角(不增添其它字母).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明从点A出发,前进10m后向右转20°,再前进10m后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.
(1)小明一共走了多少米?
(2)这个多边形的内角和是多少度?

-
科目: 来源: 题型:
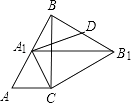
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )
A.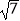
B.2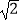
C.3
D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.

(1)求证:△ABE≌△DAF;
(2)若AF=1,四边形ABED的面积为6,求EF的长.
相关试题

