【题目】下列函数中,对于任意实数x1 , x2 , 当x1>x2时,满足y1<y2的是( )
A.y=﹣3x+2
B.y=2x+1
C.y=2x2+1
D.y=﹣ ![]()
参考答案:
【答案】A
【解析】解:A、y=﹣3x+2中k=﹣3, ∴y随x值的增大而减小,
∴A选项符合题意;
B、y=2x+1中k=2,
∴y随x值的增大而增大,
∴B选项不符合题意;
C、y=﹣2x2+1中a=﹣2,
∴当x<0时,y随x值的增大而增大,当x>0时,y随x值的增大而减小,
∴C选项不符合题意;
D、y=﹣ ![]() 中k=﹣1,
中k=﹣1,
∴当x<0时,y随x值的增大而增大,当x>0时,y随x值的增大而增大,
∴D选项不符合题意.
故选A.
【考点精析】本题主要考查了一次函数的性质和反比例函数的性质的相关知识点,需要掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列条件中,不能证明△ABD≌△ACD的条件是( )
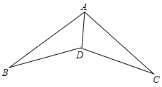
A. ∠B=∠C,BD=DC B. ∠ADB=∠ADC,BD=DC
C. ∠B=∠C,∠BAD=∠CAD D. BD=DC,AB=AC
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列证明过程:
如图,∠1=∠2,AC平分∠DAB.

求证:DC∥AB.
证明:因为AC平分∠DAB(已知),
所以∠1=∠3(_____________ ).
又因为∠1=∠2(____________),
所以∠2=∠3(______________),
所以DC∥AB(________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD丄AC 于D,EF丄AC 于F.∠AMD=∠AGF.∠1=∠2=35°
(1)求∠GFC的度数:
(2)求证:DM∥BC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:①∠MAD=∠AND;②CP=b﹣
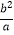 ;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是( )
;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是( )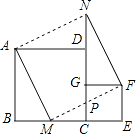
A.2
B.3
C.4
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如下图所示,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.DE=6cm,AD=9cm,则BE的长是( )
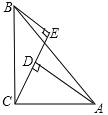
A. 6cm B. 1.5cm C. 3cm D. 4.5cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列图形,它是把一个三角形分别连接这个三角形三边的中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,…将这种做法继续下去(如图2,图3…),则图6中挖去三角形的个数为( )
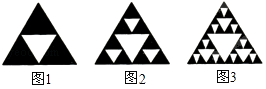
A.121
B.362
C.364
D.729
相关试题

