【题目】如图(a),(b),(c)所示,点E、D分别是正![]() 、正四边形ABCM,正五边形ABCMN钟以C点为顶点的相邻两边上的点,且
、正四边形ABCM,正五边形ABCMN钟以C点为顶点的相邻两边上的点,且![]() ,DB交AE于点P.
,DB交AE于点P.
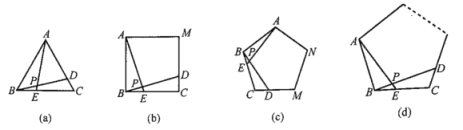
(1)在图(a)中,求![]() 的度数.
的度数.
(2)在图(b)中,![]() 的度数为________,图(c)中,
的度数为________,图(c)中,![]() 的度数为________.
的度数为________.
(3)根据前面探索,你能否将本题推广到一般的正n边形情况.若能,写出推广问题和结论;若不能,请说明理由.
参考答案:
【答案】(1)证明见解析;(2)![]() ,
,![]() ;(3)见解析
;(3)见解析
【解析】
(1)根据SAS证明![]() ,得出
,得出![]() ,再根据
,再根据![]() 计算得出
计算得出![]() 的度数;
的度数;
(2)方法与(1)相同;
(3)由(1)、(2)可得出规律:![]() 等于这个正n边形的一个内角的度数.
等于这个正n边形的一个内角的度数.
(1)∵△ABC是正三角形,
∴AB=BC,∠ABE=∠C=![]() ,
,
在![]() 和
和![]() 中
中
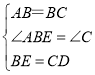 ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
(2)如图(b):
∵△ABCM是正四边形,
∴AB=BC,∠ABE=∠C=![]() ,
,
在![]() 和
和![]() 中
中
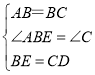 ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
如图(c):
∵△ABCMN是正五边形,
∴AB=BC,∠ABE=∠C=![]() ,
,
在![]() 和
和![]() 中
中
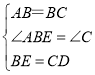 ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
(3)问题:如图(d)所示,点E,D分别是正n边形中以C点为顶点的相邻两边上的点,
且![]() ,DB交AE于P点.则
,DB交AE于P点.则![]() 等于这个正n边形的一个内角的度数,即
等于这个正n边形的一个内角的度数,即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, AB∥CD, AC∥BD, AD与BC交于O, AE⊥BC于E, DF⊥BC于F, 那么图中全等的三角形有 ( )
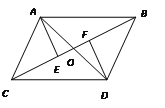
A.5对B.6对C.7对D.8对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
 中,
中, .现想利用三角形全等证明
.现想利用三角形全等证明 ,则图中所添加的辅助线应是___________.
,则图中所添加的辅助线应是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在
 中,
中,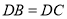 ,
,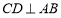 于点D,BE平分
于点D,BE平分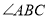 ,且
,且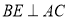 于点E与CD相交于点F,
于点E与CD相交于点F,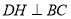 于点H,交BE于点G,下列结论:①
于点H,交BE于点G,下列结论:①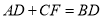 ;②
;②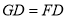 ;③
;③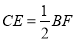 ④
④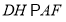 ;其中正确的是___________.
;其中正确的是___________.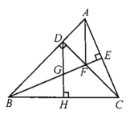
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在
 中,
中, ,
, ,D是斜边AB上任一点,
,D是斜边AB上任一点, 于E,
于E, 交CD的延长线于点F.
交CD的延长线于点F. 于点H,交AE于点G.
于点H,交AE于点G.
(1)直接写出EF、AE和BF之间的关系;
(2)探究BD与CG之间的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等.那么在什么情况下,它们会全等?
(1)阅读与证明:
对于这两个三角形均为直角三角形,显然它们全等.
对于这两个三角形均为钝角三角形,可证它们全等(证明略).
对于这两个三角形均为锐角三角形,它们也全等,可证明如下:
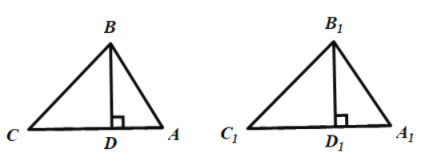
如图所示,
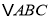 、
、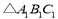 均为锐角三角形,
均为锐角三角形,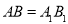 ,
, ,
,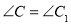 .
.求证:
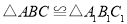 .
.证明:分别过点B,
 作
作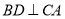 于点D,
于点D,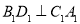 于点
于点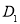 .
.∴
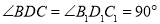 .
.在
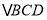 和
和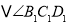 ,
,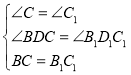
∴
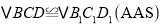 .
.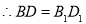 .
.____________________________________________________________.
(请你将上述证明过程补充完整)
(2)归纳与叙述:由(1)可得到一个正确结论,请你写出这个结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D,E分别在AC,AB上.

【1】(1) 已知,BD=CE,CD=BE,求证:AB=AC;
【2】(2) 分别将“BD=CE”记为①,“CD=BE” 记为②,“AB=AC”记为③.添加条件①、③,以②为结论构成命题1,添加条件②、③以①为结论构成命题2.命题1是命题2的 命题,命题2是
命题.(选择“真”或“假”填入空格).
相关试题

