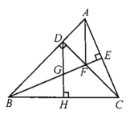
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() 于点D,BE平分
于点D,BE平分![]() ,且
,且![]() 于点E与CD相交于点F,
于点E与CD相交于点F,![]() 于点H,交BE于点G,下列结论:①
于点H,交BE于点G,下列结论:①![]() ;②
;②![]() ;③
;③![]() ④
④![]() ;其中正确的是___________.
;其中正确的是___________.
参考答案:
【答案】①②③④
【解析】
先根据AAS证明△ADC≌△FDB,得到AD=DF,∠DAC=∠DFB,从而得出①正确;
在Rt△ADF中,由AD=DF求得∠DFA![]() ,根据等腰直角三角形的性质求得∠HDC=
,根据等腰直角三角形的性质求得∠HDC=![]() ,从而得到∠DFA=∠HDC,由平行线的判定得到④正确;
,从而得到∠DFA=∠HDC,由平行线的判定得到④正确;
根据ASA证明△ABE≌△CBE,得到CE=![]() AC,结合①中证明△ADC≌△FDB可得AC=BF,则得出③正确;
AC,结合①中证明△ADC≌△FDB可得AC=BF,则得出③正确;
由等腰三角形的性质、角平分线的性质和三角形内角和定理求得∠DFB![]() ,由等腰三角形的性质、角平分线的性质和三角形外角性质求得∠DGF=
,由等腰三角形的性质、角平分线的性质和三角形外角性质求得∠DGF=![]() ,从而得到∠DFB=∠DGF,再由等角对等边得到②正确.
,从而得到∠DFB=∠DGF,再由等角对等边得到②正确.
∵![]() 于点D,
于点D,![]() 于点E,
于点E,
∴∠BDF=∠BDA=![]() ,∠BAC+∠ABF=∠DAC+∠ACD=
,∠BAC+∠ABF=∠DAC+∠ACD=![]() ,
,
∴∠ABF=∠ACD,
在△ADC和△FDB中
 ,
,
∴△ADC≌△FDB(AAS),
∴AD=DF,∠DAC=∠DFB,
又∵DF+CF=CD,CD=BD,
∴![]() ,故①正确;
,故①正确;
∵AD=DF,![]() 于点D,
于点D,
∴∠DAF=∠DFA=![]() ,
,
∵BD=DC,![]() 于点D,
于点D,![]() 于点H,
于点H,
∴∠HDC=∠HDB=![]() ,
,
又∵∠DFA![]() ,
,
∴∠DFA=∠HDC,
∴![]() ,故④正确;
,故④正确;
∵BE平分![]() ,且
,且![]() 于点E,
于点E,
∴∠ABE=∠CBE,∠AEB=∠CEB,
在△ABE和△CBE中
 ,
,
∴△ABE≌△CBE,
∴AE=CE,
∴CE=![]() AC,
AC,
又∵△ADC≌△FDB,
∴BF=AC,
∴![]() ,故③正确;
,故③正确;
∵![]() ,
,![]() 于点D,
于点D,
∴∠DBC=![]() ,
,
又∵BE平分![]() ,
,
∴∠DBE=![]() ,
,
∴∠DFB=![]() ,
,
又∵∠HDB=![]() ,
,

∴∠DGF=∠DBG+∠BDG=![]() +
+![]() =
=![]() ,
,
∴∠DFB=∠DGF,
∴DG=DF,故②正确.
故答案为:①②③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.

(1)如图1,直接写出∠A和∠C之间的数量关系___;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E. F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, AB∥CD, AC∥BD, AD与BC交于O, AE⊥BC于E, DF⊥BC于F, 那么图中全等的三角形有 ( )
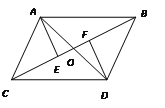
A.5对B.6对C.7对D.8对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
 中,
中, .现想利用三角形全等证明
.现想利用三角形全等证明 ,则图中所添加的辅助线应是___________.
,则图中所添加的辅助线应是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(a),(b),(c)所示,点E、D分别是正
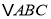 、正四边形ABCM,正五边形ABCMN钟以C点为顶点的相邻两边上的点,且
、正四边形ABCM,正五边形ABCMN钟以C点为顶点的相邻两边上的点,且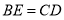 ,DB交AE于点P.
,DB交AE于点P.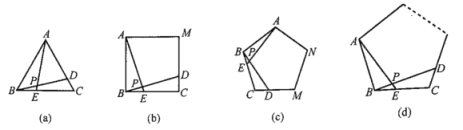
(1)在图(a)中,求
 的度数.
的度数.(2)在图(b)中,
 的度数为________,图(c)中,
的度数为________,图(c)中, 的度数为________.
的度数为________.(3)根据前面探索,你能否将本题推广到一般的正n边形情况.若能,写出推广问题和结论;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在
 中,
中, ,
, ,D是斜边AB上任一点,
,D是斜边AB上任一点, 于E,
于E, 交CD的延长线于点F.
交CD的延长线于点F. 于点H,交AE于点G.
于点H,交AE于点G.
(1)直接写出EF、AE和BF之间的关系;
(2)探究BD与CG之间的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等.那么在什么情况下,它们会全等?
(1)阅读与证明:
对于这两个三角形均为直角三角形,显然它们全等.
对于这两个三角形均为钝角三角形,可证它们全等(证明略).
对于这两个三角形均为锐角三角形,它们也全等,可证明如下:
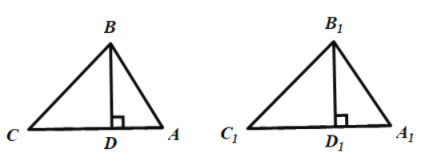
如图所示,
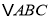 、
、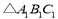 均为锐角三角形,
均为锐角三角形,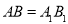 ,
, ,
,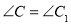 .
.求证:
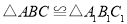 .
.证明:分别过点B,
 作
作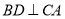 于点D,
于点D,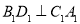 于点
于点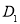 .
.∴
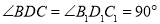 .
.在
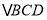 和
和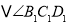 ,
,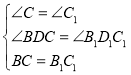
∴
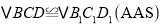 .
.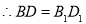 .
.____________________________________________________________.
(请你将上述证明过程补充完整)
(2)归纳与叙述:由(1)可得到一个正确结论,请你写出这个结论.
相关试题

