搜索
【题目】如图所示，我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度．小宇同学在A处观测对岸C点，测得∠CAD=45°，小英同学在距A处50米远的B处测得∠CBD=30°，请你根据这些数据算出河宽．（精确到0.01米，参考数据 
≈1.414， 
≈1.732） 
参考答案：
【答案】解：过C作CE⊥AB于E，设CE=x米， 在Rt△AEC中：∠CAE=45°，AE=CE=x
在Rt△BCE中：∠CBE=30°，BE= 
CE= x，
∴ x=x+50解之得：x=25 +25≈68.31．
答：河宽为68.31米．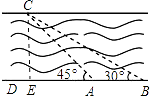
【解析】设河宽为未知数，那么可利用三角函数用河宽表示出AE、EB，然后根据BE﹣AE=50就能求得河宽．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校为了解七年级学生期中考试数学成绩情况，从中抽取了部分学生的数学成绩进行调查，规定
满分为100分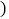
；A等为90分
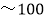分，B等为80分
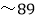分；C等为60分
分；D等是60分以下不含60分，并根据调查结果制成如下不完整的统计图：
本次抽查了______名七年级学生；
补全条形统计图；
求扇形统计图中表示“C等”部分的扇形的中心角度数；
结合统计图，写出两条正确的结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图：请你添加一个条件_____可以得到
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们用[a]表示不大于a的最大整数，例如：[2.5]＝2，[3]＝3，[－2.5]＝－3；用＜a＞表示大于a的最小整数，例如：＜2.5＞＝3，＜3＞＝4，＜－2.5＞＝－2.根据上述规定，解决下列问题：
(1)[－4.5]＝______，＜3.01＞＝____；
(2)若x为整数，且[x]＋＜x＞＝2 017，求x的值；
(3)若x，y满足方程组
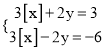，求x，y的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，OA，OD是⊙O半径，过A作⊙O的切线，交∠AOD的平分线于点C，连接CD，延长AO交⊙O于点E，交CD的延长线于点B
（1）求证：直线CD是⊙O的切线；
（2）如果D点是BC的中点，⊙O的半径为3cm，求
的长度（结果保留π） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=x+2与抛物线y=ax2+bx+6（a≠0）相交于A（
， 
）和B（4，m），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．
（1）求抛物线的解析式；
（2）是否存在这样的P点，使线段PC的长有最大值？若存在，求出这个最大值；若不存在，请说明理由；
（3）求△PAC为直角三角形时点P的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，把矩形纸片ABCD沿对角线折叠，设重叠部分为△EBD，那么下列说法错误的是（ ）
A. △EBD是等腰三角形，EB=ED B. 折叠后∠ABE和∠C′BD一定相等
C. 折叠后得到的图形是轴对称图形 D. △EBA和△EDC′一定是全等三角形
相关试题
