【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( ![]() ,
, ![]() )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)求△PAC为直角三角形时点P的坐标.
参考答案:
【答案】
(1)
解:∵B(4,m)在直线y=x+2上,
∴m=4+2=6,
∴B(4,6),
∵A( ![]() ,
, ![]() )、B(4,6)在抛物线y=ax2+bx+6上,
)、B(4,6)在抛物线y=ax2+bx+6上,
∴ 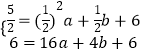 ,解得
,解得 ![]() ,
,
∴抛物线的解析式为y=2x2﹣8x+6
(2)
解:设动点P的坐标为(n,n+2),则C点的坐标为(n,2n2﹣8n+6),
∴PC=(n+2)﹣(2n2﹣8n+6),
=﹣2n2+9n﹣4,
=﹣2(n﹣ ![]() )2+
)2+ ![]() ,
,
∵PC>0,
∴当n= ![]() 时,线段PC最大且为
时,线段PC最大且为 ![]()
(3)
解:∵△PAC为直角三角形,
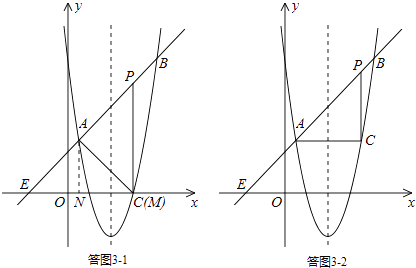
i)若点P为直角顶点,则∠APC=90°.
由题意易知,PC∥y轴,∠APC=45°,因此这种情形不存在;
ii)若点A为直角顶点,则∠PAC=90°.
如答图3﹣1,过点A( ![]() ,
, ![]() )作AN⊥x轴于点N,则ON=
)作AN⊥x轴于点N,则ON= ![]() ,AN=
,AN= ![]() .
.
过点A作AM⊥直线AB,交x轴于点M,则由题意易知,△AMN为等腰直角三角形,
∴MN=AN= ![]() ,∴OM=ON+MN=
,∴OM=ON+MN= ![]() +
+ ![]() =3,
=3,
∴M(3,0).
设直线AM的解析式为:y=kx+b,
则: 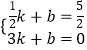 ,解得
,解得 ![]() ,
,
∴直线AM的解析式为:y=﹣x+3 ①
又抛物线的解析式为:y=2x2﹣8x+6 ②
联立①②式,解得:x=3或x= ![]() (与点A重合,舍去)
(与点A重合,舍去)
∴C(3,0),即点C、M点重合.
当x=3时,y=x+2=5,
∴P1(3,5);
iii)若点C为直角顶点,则∠ACP=90°.
∵y=2x2﹣8x+6=2(x﹣2)2﹣2,
∴抛物线的对称轴为直线x=2.
如答图3﹣2,作点A( ![]() ,
, ![]() )关于对称轴x=2的对称点C,
)关于对称轴x=2的对称点C,
则点C在抛物线上,且C( ![]() ,
, ![]() ).
).
当x= ![]() 时,y=x+2=
时,y=x+2= ![]() .
.
∴P2( ![]() ,
, ![]() ).
).
∵点P1(3,5)、P2( ![]() ,
, ![]() )均在线段AB上,
)均在线段AB上,
∴综上所述,△PAC为直角三角形时,点P的坐标为(3,5)或( ![]() ,
, ![]() )
)
【解析】(1)已知B(4,m)在直线y=x+2上,可求得m的值,抛物线图象上的A、B两点坐标,可将其代入抛物线的解析式中,通过联立方程组即可求得待定系数的值.(2)要弄清PC的长,实际是直线AB与抛物线函数值的差.可设出P点横坐标,根据直线AB和抛物线的解析式表示出P、C的纵坐标,进而得到关于PC与P点横坐标的函数关系式,根据函数的性质即可求出PC的最大值.(3)当△PAC为直角三角形时,根据直角顶点的不同,有三种情形,需要分类讨论,分别求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用<a>表示大于a的最小整数,例如:<2.5>=3,<3>=4,<-2.5>=-2.根据上述规定,解决下列问题:
(1)[-4.5]=______,<3.01>=____;
(2)若x为整数,且[x]+<x>=2 017,求x的值;
(3)若x,y满足方程组
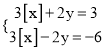 ,求x,y的取值范围.
,求x,y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度.小宇同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处50米远的B处测得∠CBD=30°,请你根据这些数据算出河宽.(精确到0.01米,参考数据
 ≈1.414,
≈1.414,  ≈1.732)
≈1.732) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OA,OD是⊙O半径,过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B

(1)求证:直线CD是⊙O的切线;
(2)如果D点是BC的中点,⊙O的半径为3cm,求 的长度(结果保留π)
的长度(结果保留π) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( )

A. △EBD是等腰三角形,EB=ED B. 折叠后∠ABE和∠C′BD一定相等
C. 折叠后得到的图形是轴对称图形 D. △EBA和△EDC′一定是全等三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数学课上,老师提出如下问题:
作图:过直线外一点作已知直线的平行线.
已知:直线l及其外一点A.
求作:l的平行线,使它经过点A.

小天利用直尺和三角板进行如下操作:如图所示:
①用三角板的斜边与已知直线l重合;
②用直尺紧靠三角板一条直角边;
③沿着直尺平移三角板,使三角板的斜边通过已知点A;
④沿着这条斜边画一条直线,所画直线与已知直线平行.
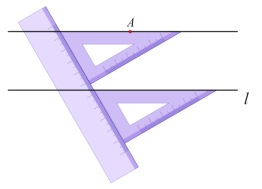
老师说:“小天的作法正确.”
请回答:小天的作图依据是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(3﹣3a,1﹣2a)在第四象限,则a的取值范围在数轴上表示正确的是( )
A.
B.
C.
D.
相关试题

