搜索
【题目】如图，把矩形纸片ABCD沿对角线折叠，设重叠部分为△EBD，那么下列说法错误的是（ ）
A. △EBD是等腰三角形，EB=ED B. 折叠后∠ABE和∠C′BD一定相等
C. 折叠后得到的图形是轴对称图形 D. △EBA和△EDC′一定是全等三角形
参考答案：
【答案】B
【解析】解：由题意得：△BC′D≌△BFD，∴DC′=DF，∠C′=∠C=90°，∠C′BD=∠CBD；
又∵四边形ABCD为矩形，∴∠A=∠F=90°；DE∥BF，AB=DF，∴∠EDB=∠FBD，DC′=AB，∴∠EDB=∠C′BD，∴EB=ED，△EBD为等腰三角形．
在△ABE与△CDE中，∵BE=DE，AB=C′D，∴△ABE≌△C′DE（HL）；
又∵△EBD为等腰三角形，∴折叠后得到的图形是轴对称图形．
综上所述：选项A、C、D成立，∴说法错误的是B．故选B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度．小宇同学在A处观测对岸C点，测得∠CAD=45°，小英同学在距A处50米远的B处测得∠CBD=30°，请你根据这些数据算出河宽．（精确到0.01米，参考数据
≈1.414， 
≈1.732） 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，OA，OD是⊙O半径，过A作⊙O的切线，交∠AOD的平分线于点C，连接CD，延长AO交⊙O于点E，交CD的延长线于点B
（1）求证：直线CD是⊙O的切线；
（2）如果D点是BC的中点，⊙O的半径为3cm，求
的长度（结果保留π） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=x+2与抛物线y=ax2+bx+6（a≠0）相交于A（
， 
）和B（4，m），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．
（1）求抛物线的解析式；
（2）是否存在这样的P点，使线段PC的长有最大值？若存在，求出这个最大值；若不存在，请说明理由；
（3）求△PAC为直角三角形时点P的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：
在数学课上，老师提出如下问题：
作图：过直线外一点作已知直线的平行线．
已知：直线l及其外一点A．
求作：l的平行线，使它经过点A．
小天利用直尺和三角板进行如下操作：如图所示：
①用三角板的斜边与已知直线l重合；
②用直尺紧靠三角板一条直角边；
③沿着直尺平移三角板，使三角板的斜边通过已知点A；
④沿着这条斜边画一条直线，所画直线与已知直线平行.
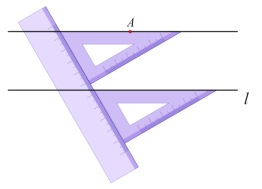
老师说：“小天的作法正确．”
请回答：小天的作图依据是___________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知点P（3﹣3a，1﹣2a）在第四象限，则a的取值范围在数轴上表示正确的是（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，A（﹣3，2），B（﹣4，﹣3），C（﹣1，﹣1）．
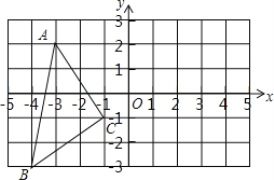
（1）在图中作出△ABC关于y轴对称的△A1B1C1；写出点△A1，B1，C1的坐标（直接写答案）：A1 ；B1 ；C1 ；
（2）△A1B1C1的面积为 ；
（3）在y轴上画出点P，使PB+PC最小．
相关试题
