【题目】正五边形广场 ![]() 的边长为
的边长为 ![]() 米,甲、乙两个同学做游戏,分别从
米,甲、乙两个同学做游戏,分别从 ![]() 、
、 ![]() 两点处同时出发,沿
两点处同时出发,沿 ![]() 的方向绕广场行走,甲的速度为
的方向绕广场行走,甲的速度为 ![]() ,乙的速度为
,乙的速度为 ![]() ,则两人第一次刚走到同一条边上时( )
,则两人第一次刚走到同一条边上时( )
A. 甲在顶点 ![]() 处 B. 甲在顶点
处 B. 甲在顶点 ![]() 处 C. 甲在顶点
处 C. 甲在顶点![]() 处 D. 甲在顶点
处 D. 甲在顶点![]() 处
处
参考答案:
【答案】D
【解析】
实际应用问题,见详解.
解:两人如果在同一条边上,说明两人的距离小于等于80米,
∵甲、乙两个同学做游戏,分别从 ![]() 、
、 ![]() 两点处同时出发,两人相差160米,甲要追回80米需要的时间是80
两点处同时出发,两人相差160米,甲要追回80米需要的时间是80![]() (50-46)=20分钟,
(50-46)=20分钟,
20分钟甲走了1000米,正好走到CD的中点设为F;20分钟乙走920米走到DE距D点40米处设为G.
甲从F走到D是40比50等于0.8分钟;乙用0.8分从G点走出0.8乘46等于36.8米距E点80-36.8-40=3.2米
由此得知甲走到D点时乙走在DE线上距E3.2米处.
∴D选项是正确的
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在抗震救灾期间承担40 000顶救灾帐篷的生产任务,分为A、B、C、D四种型号,它们的数量百分比和每天单独生产各种型号帐篷的数量如图所示:

根据以上信息,下列判断错误的是( )
A.其中的D型帐篷占帐篷总数的10%
B.单独生产B型帐篷的天数是单独生产C型帐篷天数的3倍
C.单独生产A型帐篷与单独生产D型帐篷的天数相等
D.单独生产B型帐篷的天数是单独生产A型帐篷天数的2倍 -
科目: 来源: 题型:
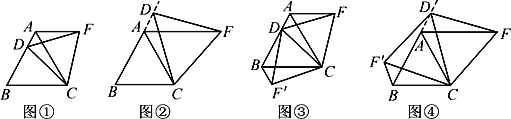
查看答案和解析>>【题目】(1)操作发现:如图①,D是等边△ABC的边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,你能发现AF与BD之间的数量关系吗?并证明你发现的结论;
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与B不重合),连接DC,以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′,连接AF,BF′,探究AF,BF′与AB有何数量关系?并证明你的探究的结论;Ⅱ.如图④,当动点D在等边△ABC的边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料: 在数学课上,老师提出如下问题:
已知:如图,四边形ABCD是平行四边形.求作:菱形AECF,使点E,F分别在BC,AD上.
小凯的作法如下:
(i)连接AC;
(ii)作AC的垂直平分线EF分别交BC,AD于E,F;
(iii)连接AE,CF.
所以四边形AECF是菱形.
老师说:“小凯的作法正确.”
请回答:在小凯的作法中,判定四边形AECF是菱形的依据是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.∠AOC=
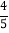 ∠COB,则∠BOF=_____°.
∠COB,则∠BOF=_____°.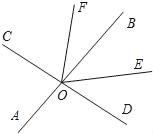
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并完成填空.
你能比较
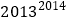 和
和 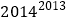 的大小吗?
的大小吗?为了解决这个问题,先把问题一般化,比较
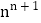 和
和 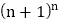 (
( 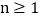 ,且
,且 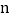 为整数)的大小.然后从分析
为整数)的大小.然后从分析 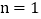 ,
,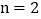 ,
,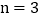
 的简单情形入手,从中发现规律,经过归纳、猜想得出结论.
的简单情形入手,从中发现规律,经过归纳、猜想得出结论.(1)通过计算(可用计算器)比较下列(1)-(7)组两数的大小:(在横线上填上 "
 ""
""  “或”
“或” ")
")(1)
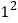
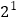 ;(2)
;(2)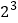
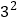 ;(3)
;(3)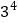
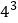 ;(4)
;(4)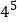
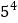 ;(5)
;(5)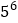
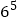 ;(6)
;(6)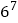
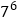 ;(7)
;(7)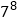
 ;
;(2)归纳第(1)问的结果,可以猜想出
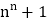 和
和 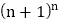 的大小关系;
的大小关系;(3)根据以上结论,可以得出
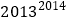 和
和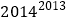 的大小关系.
的大小关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=70°,∠BCD=40°,则∠BED的度数为______.

相关试题

