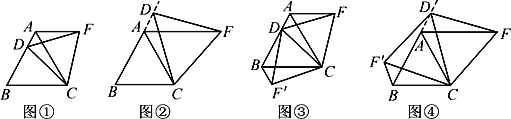
【题目】(1)操作发现:如图①,D是等边△ABC的边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,你能发现AF与BD之间的数量关系吗?并证明你发现的结论;
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与B不重合),连接DC,以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′,连接AF,BF′,探究AF,BF′与AB有何数量关系?并证明你的探究的结论;Ⅱ.如图④,当动点D在等边△ABC的边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
参考答案:
【答案】(1)AF=BD;证明见解析;(2)成立,证明见解析;(3)Ⅰ.AF+BF′=AB;证明见解析;Ⅱ.Ⅰ中的结论不成立.新的结论是AF=AB+BF′;证明见解析.
【解析】解:(1)AF=BD。证明如下:
∵△ABC是等边三角形(已知),∴BC=AC,∠BCA=60°(等边三角形的性质)。
同理知,DC=CF,∠DCF=60°。
∴∠BCA﹣∠DCA=∠DCF﹣DCA,即∠BCD=∠ACF。
在△BCD和△ACF中,∵BC=AC,∠BCD=∠ACF,DC=CF,
∴△BCD≌△ACF(SAS)。∴BD=AF(全等三角形的对应边相等)。
(2)AF=BD仍然成立。
(3)Ⅰ.AF+BF′=AB。证明如下:
由(1)知,△BCD≌△ACF(SAS),则BD=AF。
同理△BCF′≌△ACD(SAS),则BF′=AD。
∴AF+BF′=BD+AD=AB。
Ⅱ.Ⅰ中的结论不成立,新的结论是AF=AB+BF′。证明如下:
在△BCF′和△ACD中,∵BC=AC,∠BC F′=∠ACD,F′C=DC,
∴△BCF′≌△ACD(SAS)。∴BF′=AD(全等三角形的对应边相等)。
又由(2)知,AF=BD,∴AF=BD=AB+AD=AB+BF′,即AF=AB+BF′。
(1)根据等边三角形的三条边、三个内角都相等的性质,利用全等三角形的判定定理SAS可以证得△BCD≌△ACF;然后由全等三角形的对应边相等知AF=BD。
(2)通过证明△BCD≌△ACF,即可证明AF=BD。
(3)Ⅰ.AF+BF′=AB;利用全等三角形△BCD≌△ACF(SAS)的对应边BD=AF;同理△BCF′≌△ACD(SAS),则BF′=AD,所以AF+BF′=AB。
Ⅱ.Ⅰ中的结论不成立,新的结论是AF=AB+BF′:通过证明△BCF′≌△ACD(SAS),则BF′=AD(全等三角形的对应边相等),再结合(2)中的结论即可证得AF=AB+BF′
-
科目: 来源: 题型:
查看答案和解析>>【题目】在共有15人参加的“我爱祖国”演讲比赛中,参赛选手要想知道自己是否能进入前8名,只需要了解自己的成绩以及全部成绩的( )
A. 平均数 B. 众数 C. 中位数 D. 方差
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有公路l1同侧、l2异侧的两个城镇A,B,电信部门要在S区修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不写作法)

-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=﹣1是关于x的方程ax+1=2的解,则a的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列单项式:﹣a,2a2 , ﹣3a3 , 4a4 , ﹣5a5 , …可以得到第2016个单项式是;第n个单项式是 .
-
科目: 来源: 题型:
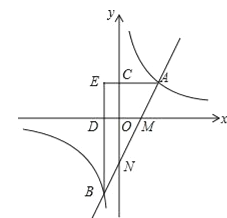
查看答案和解析>>【题目】如图,直线y=2x﹣2分别与x轴、y轴相交于M,N两点,并且与双曲线y=
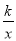 (k>0)相交于A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,AC与BD的延长线交于点E(m,n).
(k>0)相交于A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,AC与BD的延长线交于点E(m,n).(1)求证:
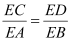 ;
;(2)若
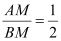 ,求
,求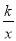 >2x﹣2的x的取值范围;
>2x﹣2的x的取值范围;(3)在(2)的条件下,P为双曲线上一点,以OB,OP为邻边作平行四边形,且平行四边形的周长最小,求第四个顶点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )

A.35°
B.45°
C.55°
D.65°
相关试题

