【题目】阅读下面材料: 在数学课上,老师提出如下问题:
已知:如图,四边形ABCD是平行四边形.求作:菱形AECF,使点E,F分别在BC,AD上.
小凯的作法如下:
(i)连接AC;
(ii)作AC的垂直平分线EF分别交BC,AD于E,F;
(iii)连接AE,CF.
所以四边形AECF是菱形.
老师说:“小凯的作法正确.”
请回答:在小凯的作法中,判定四边形AECF是菱形的依据是 . 
参考答案:
【答案】对角线互相垂直的平行四边形是菱形或有一组邻边相等的平行四边形是菱形或四条边都相等的四边形是菱形
【解析】解:由作法得EF垂直平分AC,则FA=FC,EA=EC,再证明四边形AECF为平行四边形,从而得到四边形AECF为菱形. 所以答案是对角线互相垂直的平行四边形是菱形或有一组邻边相等的平行四边形是菱形或四条边都相等的四边形是菱形.
【考点精析】本题主要考查了线段垂直平分线的性质和平行四边形的性质的相关知识点,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.
-
科目: 来源: 题型:
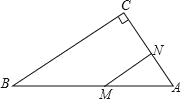
查看答案和解析>>【题目】如图,在 Rt△ABC 中,∠C=90°,∠A=60°,AB=10cm,若点M 从点 B 出发以 2cm/s 的速度向点 A 运动,点 N 从点 A 出发以 1cm/s 的速度向点 C 运动,设 M、N 分别从点 B、A 同时出发,运动的时间为 ts.
(1)用含 t 的式子表示线段 AM、AN 的长;
(2)当 t 为何值时,△AMN 是以 MN 为底边的等腰三角形?
(3)当 t 为何值时,MN∥BC?并求出此时 CN 的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在抗震救灾期间承担40 000顶救灾帐篷的生产任务,分为A、B、C、D四种型号,它们的数量百分比和每天单独生产各种型号帐篷的数量如图所示:

根据以上信息,下列判断错误的是( )
A.其中的D型帐篷占帐篷总数的10%
B.单独生产B型帐篷的天数是单独生产C型帐篷天数的3倍
C.单独生产A型帐篷与单独生产D型帐篷的天数相等
D.单独生产B型帐篷的天数是单独生产A型帐篷天数的2倍 -
科目: 来源: 题型:
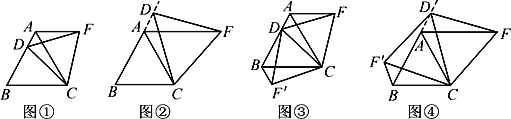
查看答案和解析>>【题目】(1)操作发现:如图①,D是等边△ABC的边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,你能发现AF与BD之间的数量关系吗?并证明你发现的结论;
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与B不重合),连接DC,以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′,连接AF,BF′,探究AF,BF′与AB有何数量关系?并证明你的探究的结论;Ⅱ.如图④,当动点D在等边△ABC的边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正五边形广场
 的边长为
的边长为 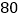 米,甲、乙两个同学做游戏,分别从
米,甲、乙两个同学做游戏,分别从 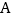 、
、 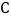 两点处同时出发,沿
两点处同时出发,沿 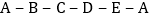 的方向绕广场行走,甲的速度为
的方向绕广场行走,甲的速度为 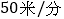 ,乙的速度为
,乙的速度为 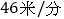 ,则两人第一次刚走到同一条边上时( )
,则两人第一次刚走到同一条边上时( )A. 甲在顶点
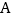 处 B. 甲在顶点
处 B. 甲在顶点 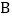 处 C. 甲在顶点
处 C. 甲在顶点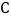 处 D. 甲在顶点
处 D. 甲在顶点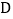 处
处 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.∠AOC=
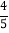 ∠COB,则∠BOF=_____°.
∠COB,则∠BOF=_____°.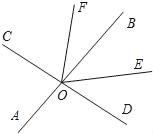
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并完成填空.
你能比较
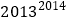 和
和 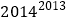 的大小吗?
的大小吗?为了解决这个问题,先把问题一般化,比较
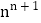 和
和 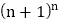 (
( 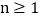 ,且
,且 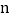 为整数)的大小.然后从分析
为整数)的大小.然后从分析 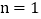 ,
,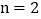 ,
,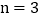
 的简单情形入手,从中发现规律,经过归纳、猜想得出结论.
的简单情形入手,从中发现规律,经过归纳、猜想得出结论.(1)通过计算(可用计算器)比较下列(1)-(7)组两数的大小:(在横线上填上 "
 ""
""  “或”
“或” ")
")(1)
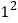
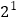 ;(2)
;(2)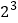
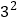 ;(3)
;(3)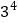
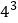 ;(4)
;(4)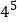
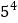 ;(5)
;(5)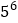
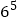 ;(6)
;(6)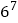
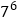 ;(7)
;(7)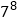
 ;
;(2)归纳第(1)问的结果,可以猜想出
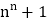 和
和 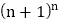 的大小关系;
的大小关系;(3)根据以上结论,可以得出
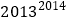 和
和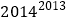 的大小关系.
的大小关系.
相关试题

