【题目】教材呈现:如图是华师版八年级上册数学教材第96页的部分内容.
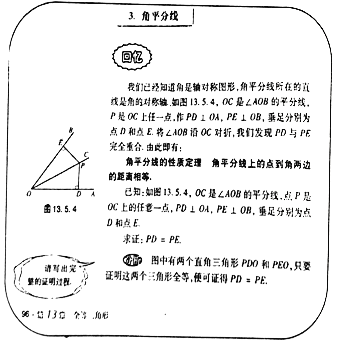

请根据教材中的分析,结合图①,写出“角平分线的性质定理”完整的证明过程.
定理应用:
如图②,在四边形ABCD中,∠B=∠C,点E在边BC上,AE平分∠BAD,DE平分∠ADC.
(1)求证:BE=CE.
(2)若四边形ABCD的周长为24,BE=2,面积为30,则△ABE的边AB的高的长为_______.
参考答案:
【答案】教材呈现:见解析;定理应用:(1)见解析;(2)3
【解析】
教材呈现:
利用AAS可证明△POD≌△POE(AAS),即可得出PD=PE;
定理应用:
(1)过E作EF⊥AB于F,EG⊥AD于G,EH⊥CD于H,由角平分线的性质定理可得EF=EG=EH,利用AAS可证明△BEF≌△CEH,得出BE=EC;
(2)利用HL可证明Rt△AEF≌Rt△AEG,得出AF=AG,同理DG=DH,由(1)得出△BEF≌△CEH,得出BF=CH,设BF=CH=x,AF=AG=y,DG=DH=z,由四边形ABCD的周长得出x+y+z=10,由四边形ABCD的面积得出(x+y+z)EF=30,求出EF=3即可.
教材呈现:角平分线的性质定理:角平分线上的点到角两边的距离相等.
已知:OC是∠AOB的平分线,点P是OC上的任意一点,PD⊥OA,PE⊥OB,垂足分别是点D和E.
求证:PD=PE.
证明:∵OC是∠AOB的平分线,
∴∠POD=∠POE,
∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°,
在△POD和△POE中, ,
,
∴△POD≌△POE(AAS),
∴PD=PE.
定理应用:
(1)过E作EF⊥AB于F,EG⊥AD于G,EH⊥CD于H,
∵AE平分∠BAD,DE平分∠ADC,
∴EF=EG=EH,
在△BEF与△CEH中, ,
,
∴△BEF≌△CEH(AAS),
∴BE=CE.

(2)解:∵EF⊥AB于F,EG⊥AD于G,EH⊥CD于H,
∵AE平分∠BAD,DE平分∠ADC,
∴EF=EG=EH,
在Rt△AEF和Rt△AEG中,![]() ,
,
∴Rt△AEF≌Rt△AEG(HL),
∴AF=AG,
同理:DG=DH,
由(1)得:△BEF≌△CEH,
∴BF=CH,
设BF=CH=x,AF=AG=y,DG=DH=z,
∵四边形ABCD的周长为24,CE=BE=2,
∴x+y+y+z+z+x+2+2=24,
∴x+y+z=10,
∵四边形ABCD的面积为30,
∴![]() (x+y)EF+
(x+y)EF+![]() (y+z)EG+
(y+z)EG+![]() (z+x)ED=30,
(z+x)ED=30,
整理得:(x+y+z)EF=30,即10×EF=30,
∴EF=3,
即△ABE的边AB的高的长为3.
故答案为:3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A,B分别是反比例函数y=
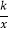 (x<0),y=
(x<0),y=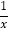 (x>0)的图象上的点,且∠AOB=90°,tan∠BAO=
(x>0)的图象上的点,且∠AOB=90°,tan∠BAO= ,则k的值为( )
,则k的值为( )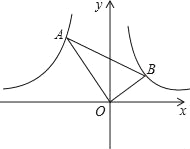
A. 2 B. ﹣2 C. 4 D. ﹣4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,E为CD中点,连接AE并延长AE交BC的延长线于点F.
(1)求证:CF=AD.
(2)若AD=3,AB=8,当BC为多少时,点B在线段AF的垂直平分线上,为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在大课间活动中,同学们积极参加体育锻炼,小龙在全校随机抽取了一部分同学就“我最喜爱的体育项目”进行了一次调查(每位同学必选且只选一项).下面是他通过收集的数据绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
(1)小龙一共抽取了 名学生.
(2)补全条形统计图;
(3)求“其他”部分对应的扇形圆心角的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,其顶点坐标为A(﹣1,﹣3),与x轴的一个交点为B(﹣3,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①abc>0;②不等式ax2+(b﹣m)x+c﹣n<0的解集为﹣3<x<﹣1;③抛物线与x轴的另一个交点是(3,0);④方程ax2+bx+c+3=0有两个相等的实数根;其中正确的是( )
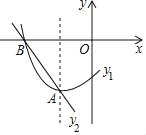
A. ①③ B. ②③ C. ③④ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆C过原点并与坐标轴分别交于A、D两点,已知点B为圆C圆周上一动点,且∠ABO=30°,点D的坐标为(0,2
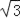 ).
).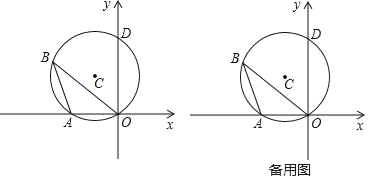
(1)直接写出圆心 C 的坐标;
(2)当△BOD为等边三角形时,求点B的坐标;
(3)若以点B为圆心、r为半径作圆B,当圆B与两个坐标轴同时相切时,求点B的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一个坡角为30°的斜坡上有一电线杆AB,当太阳光与水平线成45°角时,测得该杆在斜坡上的影长BC为20m.求电线杆AB的高(精确到0.1m,参考数值:
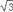 ≈1.73,
≈1.73, ≈1.41).
≈1.41).
相关试题

