【题目】如图,已知点A,B分别是反比例函数y=![]() (x<0),y=
(x<0),y=![]() (x>0)的图象上的点,且∠AOB=90°,tan∠BAO=
(x>0)的图象上的点,且∠AOB=90°,tan∠BAO=![]() ,则k的值为( )
,则k的值为( )
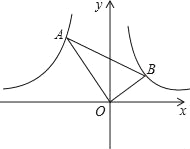
A. 2 B. ﹣2 C. 4 D. ﹣4
参考答案:
【答案】D
【解析】
首先过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,易得△OBD∽△AOC,又由点A,B分别在反比例函数y=![]() (x<0),y=
(x<0),y=![]() (x>0)的图象上,即可得S△OBD=
(x>0)的图象上,即可得S△OBD=![]() ,S△AOC=
,S△AOC=![]() |k|,然后根据相似三角形面积的比等于相似比的平方,即可求出k的值
|k|,然后根据相似三角形面积的比等于相似比的平方,即可求出k的值
解:过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,
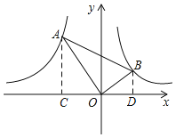
∴∠ACO=∠ODB=90°,
∴∠OBD+∠BOD=90°,
∵∠AOB=90°,
∴∠BOD+∠AOC=90°,
∴∠OBD=∠AOC,
∴△OBD∽△AOC,
又∵∠AOB=90°,tan∠BAO=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,即
,即![]() ,
,
解得k=±4,
又∵k<0,
∴k=-4,
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)求证:2CD2=AD2+DB2.

-
科目: 来源: 题型:
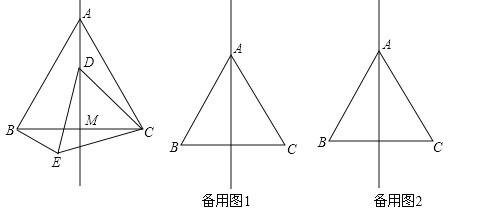
查看答案和解析>>【题目】如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.
(1)求∠CAM的度数;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①、图②均是5×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、E、F均在格点上.在图①、图②中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
(1)在图①中画一个正方形ABCD,使其面积为5.
(2)在图②中画一个等腰△EFG,使EF为其底边.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,E为CD中点,连接AE并延长AE交BC的延长线于点F.
(1)求证:CF=AD.
(2)若AD=3,AB=8,当BC为多少时,点B在线段AF的垂直平分线上,为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在大课间活动中,同学们积极参加体育锻炼,小龙在全校随机抽取了一部分同学就“我最喜爱的体育项目”进行了一次调查(每位同学必选且只选一项).下面是他通过收集的数据绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
(1)小龙一共抽取了 名学生.
(2)补全条形统计图;
(3)求“其他”部分对应的扇形圆心角的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】教材呈现:如图是华师版八年级上册数学教材第96页的部分内容.
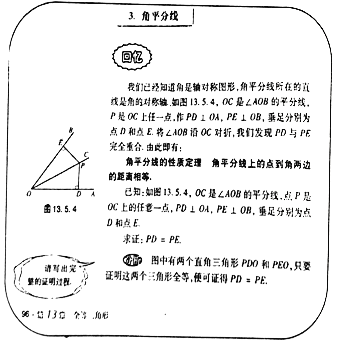

请根据教材中的分析,结合图①,写出“角平分线的性质定理”完整的证明过程.
定理应用:
如图②,在四边形ABCD中,∠B=∠C,点E在边BC上,AE平分∠BAD,DE平分∠ADC.
(1)求证:BE=CE.
(2)若四边形ABCD的周长为24,BE=2,面积为30,则△ABE的边AB的高的长为_______.
相关试题

