【题目】在大课间活动中,同学们积极参加体育锻炼,小龙在全校随机抽取了一部分同学就“我最喜爱的体育项目”进行了一次调查(每位同学必选且只选一项).下面是他通过收集的数据绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
(1)小龙一共抽取了 名学生.
(2)补全条形统计图;
(3)求“其他”部分对应的扇形圆心角的度数.

参考答案:
【答案】(1)50(2)见解析(3)64.8°
【解析】试题分析:(1)根据跳绳的人数是15,占30%,即可求得总人数;
(2)根据百分比的意义求得踢毽子的人数,则其他项目的人数可求得,从而补全直方图;
(3)利用“其他”部分对应的百分比乘以360°即可求解.
试题解析:(1)抽取的总人数是:15÷30%=50(人);
(2)踢毽子的人数是:50×20%=10(人),则其他项目的人数是:50-15-16-10=9(人),
补全条形统计图:
(3)“其他”部分对应的扇形圆心角的度数是![]() ×360°=64.8°.
×360°=64.8°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC=5,BC=6,AD⊥BC,E、F分别为AC、AD上两动点,连接CF、EF,则CF+EF的最小值为____.
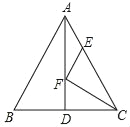
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.

(1)求点A, B的坐标;
(2)过点B作直线BP与x轴相交于点P,且使OP=2OA,求
 的面积.
的面积.(3)直接写出y<0时,x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式(组)并将解集在数轴上表示出来
(1)
 +1≥x
+1≥x(2)

分解因式
(3)m2(a﹣1)﹣2m(a﹣1)+(a﹣1)
(4)(a2﹣2ab+b2)﹣4
化简:
(5)

(6)
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,∠ACB=900,且A(0,4),点C(2,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D。
(1)求证;△AOC≌△CEB
(2)求△ABD的面积。

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是甲乙两车离A地的距离y(千米)与行驶时间x(小时)之间的函数图象.
(1)求甲车离A地的距离y甲(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(2)若它们出发第5小时时,离各自出发地的距离相等,求乙车离A地的距离y乙(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(3)在(2)的条件下,求它们在行驶的过程中相遇的时间.
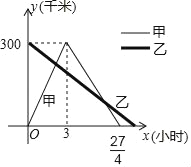
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把长方形纸片OABC放入直角坐标系中,使OA, OC分别落在x轴、y轴的正半轴上,连接AC,将
 翻折,点B落在该坐标平面内,设这个落点为D,CD交x轴于点E,已知CB=8,AB=4.
翻折,点B落在该坐标平面内,设这个落点为D,CD交x轴于点E,已知CB=8,AB=4.
(1)求AC所在直线的函数关系式;
(2)求点E的坐标和
 的面积:
的面积:(3)求点D的坐标,并判断点(8, -4)是否在直线OD上,说明理由.
相关试题

