【题目】如图,在等边三角形![]() 的顶点
的顶点![]() 、
、![]() 处各有一只蜗牛,他们同时出发,以相同的速度分别由
处各有一只蜗牛,他们同时出发,以相同的速度分别由![]() 向
向![]() ,由
,由![]() 向
向![]() 爬行,经过
爬行,经过![]() 分钟后,它们分别爬行到了
分钟后,它们分别爬行到了![]() 、
、![]() 处,设在爬行过程中
处,设在爬行过程中![]() 与
与![]() 的交点为
的交点为![]() .
.

(1)当点![]() 、
、![]() 不是
不是![]() 、
、![]() 的中点时,图中由全等三角形吗?如果没有,请说明理由;如过有,请找出所有全等三角形,并选择其中一对进行证明
的中点时,图中由全等三角形吗?如果没有,请说明理由;如过有,请找出所有全等三角形,并选择其中一对进行证明
(2)问蜗牛在爬行过程中![]() 与
与![]() 所成的大小有无变化?请证明你的结论(提示:等边三角形的三个 都相等,每个角等于
所成的大小有无变化?请证明你的结论(提示:等边三角形的三个 都相等,每个角等于![]() )
)
参考答案:
【答案】(1)有,理由见解析;(2)不变,值为120o,理由见解析
【解析】
(1)图中有全等三角形,由已知条件可知△ACD≌△CBE;△ABE≌△CBD,根据SAS即可判断出△ACD≌△CBE;
(2)根据△ACD≌△CBE,可知∠BFC=180°-∠FBC-∠BCD=180°-∠ACD-∠BCD.
(1)有全等三角形:如△ACD≌△CBE;△ABE≌△CBD,
证明:∵AB=BC=CA,两只蜗牛速度相同,且同时出发,
∴CE=AD;∠A=∠BCE=60°,
在△ACD和△CBE中,
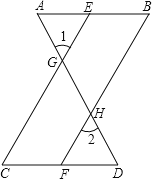
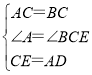 ,
,
∴△ACD≌△CBE;
(2)DC和BE所成的∠BFC的大小不变.
证明:∵△ACD≌△CBE,
∴∠BFC=180°-∠FBC-∠BCD=180°-∠ACD-∠BCD=120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),
且∠1=∠CGD( ),
∴∠2=∠CGD(等量代换),
∴CE∥BF( ),
∴∠ =∠BFD( ).
又∵∠ =∠C(已知),
∴∠BFD=∠B(等量代换),
∴AB∥CD( ).
-
科目: 来源: 题型:
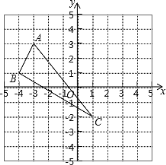
查看答案和解析>>【题目】在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1):
(1)请画出△ABC沿
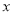 轴向右平移3个单位长度,再沿
轴向右平移3个单位长度,再沿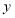 轴向上平移2个单位长度后的
轴向上平移2个单位长度后的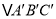 (其中
(其中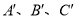 分别是A、B、C的对应点,不写画法);
分别是A、B、C的对应点,不写画法);(2)直接写出
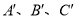 三点的坐标;
三点的坐标;(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】转盘被均匀分为37格,分别标以0~36这37个数字,且所有写有偶数(0除外)的格子都涂成了红色,写有奇数的格子都涂成了蓝色,而0所在的格子被涂成了绿色.游戏者用此转盘(如图)做游戏,每次游戏游戏者交游戏费1元,游戏时,游戏者先押一个数字,然后快速地转动转盘,若转盘停止转动时,指针所指格子中的数字恰为游戏者所押数字,则游戏者将获得奖励36元,该游戏对游戏者有利吗?转动多次后,游戏者平均每次将获得或损失多少元?
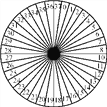
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了了解在校学生对校本课程的喜爱情况,随机调查了九年级学生对A,B,C,D,E五类校本课程的喜爱情况,要求每位学生只能选择一类最喜欢的校本课程,根据调查结果绘制了如下的两个统计图.
请根据图中所提供的信息,完成下列问题:
(1)本次被调查的学生的人数为 ;
(2)补全条形统计图;
(3)扇形统计图中,C类所在扇形的圆心角的度数为 ;
(4)若该中学有4000名学生,请估计该校喜爱C,D两类校本课程的学生共有多少名.
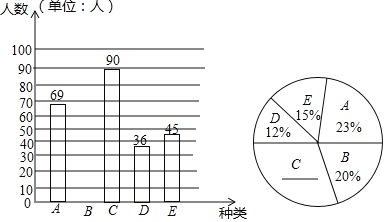
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为开展体育大课间活动,需要购买篮球与足球若干个.已知购买2个篮球和3个足球共需要380元;购买4个篮球和5个足球共需要700元.
(1)求购买一个篮球、一个足球各需多少元?
(2)若体育老师带了6000元去购买这种篮球与足球共80个.由于数量较多,店主给出“一律打九折”的优惠价,那么他最多能购买多少个篮球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC的周长为21cm,AB=6cm,BC边上中线AD=5cm,△ACD周长为16cm,则AC的长为__________cm.

相关试题

