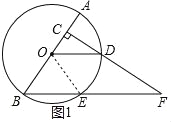
【题目】如图,AB是⊙O的直径,且AB=4,点C在半径OA上(点C与点O、A不重合),过点C作AB的垂线交⊙O于点D,连接OD,过点B作OD的平行线交⊙O于点E,交CD的延长线于点F.
(1)若∠F=30°,请证明E是![]() 的中点;
的中点;
(2)若AC=![]() ,求BEEF的值.
,求BEEF的值.

参考答案:
【答案】(1)证明见解析;(2)BEEF=5.
【解析】
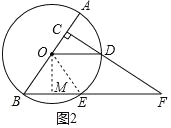
(1)连接OE,如图1所示,根据已知条件易证△OBE为等边三角形,即可得∠OEB=∠BOE=60°.又因OD∥BF,根据平行线的性质可得∠DOE=∠BEO=∠BOE=60°,即可得![]() ;(2)过点Q作OM⊥BE于M,如图2所示,先证明△OBM≌△DOC,可得BE=2OC=3;再证明△COD∽△CBF,根据相似三角形的性质求得BF=
;(2)过点Q作OM⊥BE于M,如图2所示,先证明△OBM≌△DOC,可得BE=2OC=3;再证明△COD∽△CBF,根据相似三角形的性质求得BF=![]() ,即可得EF=BF﹣BE=
,即可得EF=BF﹣BE=![]() ,所以BEEF=3×
,所以BEEF=3×![]() =5.
=5.
(1)证明:连接OE,如图1所示.
∵CF⊥AB,
∴∠FCB=90°.
∵∠F=30°,
∴∠OBE=60°.
∵OB=OE,
∴△OBE为等边三角形,
∴∠OEB=∠BOE=60°.
∵OD∥BF,
∴∠DOE=∠BEO=∠BOE=60°,
∴![]() =
=![]() .
.
(2)过点Q作OM⊥BE于M,如图2所示.
∵OB=OE,
∴BE=2BM.
∵OD∥BF,
∴∠COD=∠B.
在△OBM和△DOC中,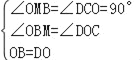 ,
,
∴△OBM≌△DOC(AAS),
∴BM=OC=2﹣![]() =
=![]() ,
,
∴BE=2OC=3.
∵OD∥BF,
∴△COD∽△CBF,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴BF=![]() ,
,
∴EF=BF﹣BE=![]() ﹣3=
﹣3=![]() ,
,
∴BEEF=3×![]() =5.
=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大刚在晚上由灯柱A走向灯柱B,当他走到M点时,发觉他身后影子的顶部刚好接触到灯柱A的底部,当他向前再走12米到N点时,发觉他身前的影子刚好接触到灯柱B的底部,已知大刚的身高是1.6米,两根灯柱的高度都是9.6米,设AM=NB=x米.求:两根灯柱之间的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠BAC=90°,AB=AC,D、E是BC边上的点,将△ABD绕点A旋转,得到△ACD′.

(1)求∠DAD′的度数。
(2)当∠DAE=45°时,求证:DE=D′E;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,DE∥AB,EF∥AB,∠BED=∠CEF,
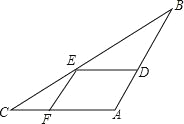
(1)试说明△ABC是等腰三角形,
(2)探索AB+AC与四边形ADEF的周长关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫做△ABC的费马点.
(1)如果点P为锐角△ABC的费马点,且∠ABC=60°.
①求证:△ABP∽△BCP;
②若PA=3,PC=4,则PB= .
(2)已知锐角△ABC,分别以AB、AC为边向外作正△ABE和正△ACD,CE和BD 相交于P点.如图(2)
①求∠CPD的度数;
②求证:P点为△ABC的费马点.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A. 了解全市中学生对泰州“三个名城”含义的知晓度的情况,适合用抽样调查
B. 若甲组数据方差S甲2=0.39,乙组数据方差S乙2=0.27,则乙组数据比甲组数据稳定
C. 某种彩票中奖的概率是
 ,买100张该种彩票一定会中奖
,买100张该种彩票一定会中奖D. 数据﹣1、1.5、2、2、4的中位数是2
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)请用两种不同的方法列代数式表示图中阴影部分的面积.

方法①_________________;
方法②_________________;
(2)根据(1)写出一个等式________________;
(3)若
 ,
, .
.①求
 的值。
的值。②
 ,
, 的值.
的值.
相关试题

