【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F. 
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.
参考答案:
【答案】
(1)解:∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,
∴DE=CE,OE=OE,
∴Rt△ODE≌Rt△OCE,
∴OD=OC,
∴△DOC是等腰三角形,
∵OE是∠AOB的平分线,
∴OE是CD的垂直平分线
(2)解:∵OE是∠AOB的平分线,∠AOB=60°,
∴∠AOE=∠BOE=30°,
∵EC⊥OB,ED⊥OA,
∴OE=2DE,∠ODF=∠OED=60°,
∴∠EDF=30°,
∴DE=2EF,
∴OE=4EF
【解析】(1)先根据E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA得出△ODE≌△OCE,可得出OD=OC,DE=CE,OE=OE,可得出△DOC是等腰三角形,由等腰三角形的性质即可得出OE是CD的垂直平分线;(2)先根据E是∠AOB的平分线,∠AOB=60°可得出∠AOE=∠BOE=30°,由直角三角形的性质可得出OE=2DE,同理可得出DE=2EF即可得出结论.
【考点精析】本题主要考查了线段垂直平分线的性质的相关知识点,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线
 的一部分,请根据图中信息解答下列问题:
的一部分,请根据图中信息解答下列问题:(1)求k的值;
(2)恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时?

-
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)A,B间的距离是;
(2)若点C也是数轴上的点,C到B的距离是C到原点O的距离的3倍,求C对应的数;
(3)若当电子P从B点出发,以6个单位长度/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4个单位长度/秒的速度向左运动,设两只电子蚂蚁在数轴上的D点相遇,那么D点对应的数是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2+2ab+a.
如:1☆3=1×32+2×1×3+1=16.
(1)求(﹣2)☆3的值;
(2)若(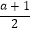 ☆3)☆(﹣
☆3)☆(﹣  )=8,求a的值;
)=8,求a的值;
(3)若2☆x=m,( x)☆3=n(其中x为有理数),试比较m,n的大小.
x)☆3=n(其中x为有理数),试比较m,n的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,梯形ABCD中,AD∥BC,P是AB的中点,过P点作AD的平行线交DC于Q点.

(1)PQ与BC平行吗?为什么?
(2)测DQ与CQ的长,是否相等? -
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列要求画图.
(1)如图(1)所示,过点A画MN∥BC;
(2)如图(2)所示,过点P画PE∥OA,交OB于点E,过点P画PH∥OB,交OA于点H;
(3)如图(3)所示,过点C画CE∥DA,与AB交于点E,过点C画CF∥DB,与AB的延长线交于点F.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列直线中,经过第一、二、三象限的是( )
A. 直线y= x-1 ; B. 直线y= -x+1; C. 直线y=x+1; D. 直线y=-x-1 .
相关试题

