搜索
【题目】如图所示，梯形ABCD中，AD∥BC，P是AB的中点，过P点作AD的平行线交DC于Q点．
（1）PQ与BC平行吗？为什么？
（2）测DQ与CQ的长，是否相等？
参考答案：
【答案】
（1）解：平行．∵PQ∥AD，AD∥BC，
∴PQ∥BC
（2）解：DQ=CQ
【解析】（1）根据平行公理平行于同一直线的两条直线互相平行得出结论PQ∥BC。
（2）DQ=CQ，根据平行线等分线段定理。如果一组平行线在一条直线上截出的线段相等，那么在其他直线上截得的线段也相等。即可得出结论。
【考点精析】本题主要考查了平行公理和平行线分线段成比例的相关知识点，需要掌握平行公理――平行线的存在性与惟一性;经过直线外一点，有且只有一条直线与这条直线平行;如果两条直线都与第三条直线平行，那么这两条直线也互相平行；三条平行线截两条直线，所得的对应线段成比例才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】
（1）A，B间的距离是；
（2）若点C也是数轴上的点，C到B的距离是C到原点O的距离的3倍，求C对应的数；
（3）若当电子P从B点出发，以6个单位长度/秒的速度向左运动，同时另一只电子蚂蚁Q恰好从A点出发，以4个单位长度/秒的速度向左运动，设两只电子蚂蚁在数轴上的D点相遇，那么D点对应的数是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】用“☆”定义一种新运算：对于任意有理数a和b，规定a☆b=ab2+2ab+a．
如：1☆3=1×32+2×1×3+1=16．
（1）求（﹣2）☆3的值；
（2）若（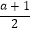
☆3）☆（﹣ 
）=8，求a的值；
（3）若2☆x=m，（
x）☆3=n（其中x为有理数），试比较m，n的大小． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知：E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C、D是垂足，连接CD，且交OE于点F．
（1）求证：OE是CD的垂直平分线．
（2）若∠AOB=60°，请你探究OE，EF之间有什么数量关系？并证明你的结论． -
科目： 来源： 题型：
查看答案和解析>>【题目】根据下列要求画图．
（1）如图(1)所示，过点A画MN∥BC；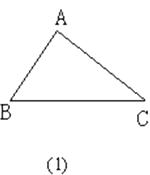
（2）如图(2)所示，过点P画PE∥OA，交OB于点E，过点P画PH∥OB，交OA于点H；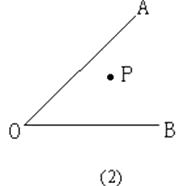
（3）如图(3)所示，过点C画CE∥DA，与AB交于点E，过点C画CF∥DB，与AB的延长线交于点F．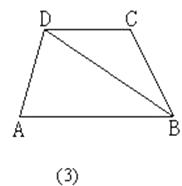
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列直线中，经过第一、二、三象限的是（ ）
A. 直线y= x－1 ； B. 直线y= －x+1； C. 直线y=x+1； D. 直线y=－x－1 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了解今年初三学生的数学学习情况，某校在第一轮模拟测试后，对初三全体同学的数学成绩作了统计分析，绘制如下图表：请结合图表所给出的信息解答系列问题：
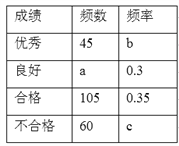
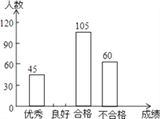
(1)该校初三学生共有多少人?
(2)求表中a，b，c的值，并补全条形统计图.
(3)初三(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍，求恰好选中甲、乙两位同学的概率.
相关试题
