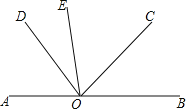
【题目】如图,已知,A、O、B在同一条直线上,∠AOE=∠COD,∠EOD=30°.
(1)若∠AOE=88°30′,求∠BOC的度数;
(2)若射线OC平分∠EOB,求∠BOC的度数.
参考答案:
【答案】(1) 33°;(2) ∠BOC=50°
【解析】
(1)先求出∠AOC度数,再利用∠AOC与∠BOC互补关系求解;
(2)由∠AOE=∠COD,易得∠AOD=∠COE,再借助角平分线定义分析出∠AOD=∠COE=∠BOC,根据这三个等角加上∠DOE等于180°列方程,从而可求出∠BOC度数.
(1)∵∠AOC=∠AOE+∠DOC-∠DOE =88°30′+88°30′-30°=147°,
∴∠BOC=180°-∠AOC =180°-147°=33°;
(2)∵∠AOE=∠COD,
∴∠AOE-∠DOE=∠COD-∠DOE,
即∠AOD=∠COE,
∵OC平分∠BOE,
∴∠BOC=∠COE,
∴∠BOC=∠COE=∠AOD,
设∠BOC=∠COE=∠AOD=x°,
则3x+30°=180°,解得x=50°,
所以∠BOC=50°.
-
科目: 来源: 题型:
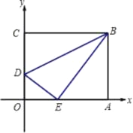
查看答案和解析>>【题目】将一矩形纸片OABC放在平面直角坐标系中,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=8,如图在OC边上取一点D,将△BCD沿BD折叠,使点C恰好落在OA边上,记作E点;
(1)求点E的坐标及折痕DB的长;
(2)在x轴上取两点M、N(点M在点N的左侧),且MN=4.5,求使四边形BDMN的周长最短的点M、点N的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将1,
 ,
,  ,
,  按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,2)表示的两数之积是 _________.
按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,2)表示的两数之积是 _________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ABC=∠DCB,添加一个条件,使△ABC≌△DCB,你添加的条件是_____.(注:只需写出一个条件即可)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=90°,AB=3,BC=2,点O在AC边上,⊙O与AB、BC分别切于点D、E,则⊙O的半径长为 .

-
科目: 来源: 题型:
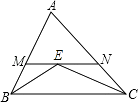
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB,AC于M、N,则△AMN的周长为( )
A.12
B.4
C.8
D.不确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好地治理水质,保护环境,某污水处理公司决定购买10台污水处理设备,现有A、B两种设备可供选择,月处理污水分别为240m3/月、200m3/月.经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少8万元.
(1)A、B两种型号的设备每台的价格是多少?
(2)若污水处理公司购买设备的预算资金不超过125万元,你认为该公司有哪几种购买方案?
(3)若每月需处理的污水约2040m3,在不突破(2)中资金预算的前提下,为了节约资金,又要保证治污效果,请你为污水处理公司设计一种最省钱的方案.
相关试题

