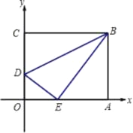
【题目】将一矩形纸片OABC放在平面直角坐标系中,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=8,如图在OC边上取一点D,将△BCD沿BD折叠,使点C恰好落在OA边上,记作E点;
(1)求点E的坐标及折痕DB的长;
(2)在x轴上取两点M、N(点M在点N的左侧),且MN=4.5,求使四边形BDMN的周长最短的点M、点N的坐标。
参考答案:
【答案】(1)E(4,0);DB=5![]() ;(2)M(1.5,0);N(6,0);
;(2)M(1.5,0);N(6,0);
【解析】
(1)、根据矩形的性质得到BC=OA=10,AB=OC=8,再根据折叠的性质得到BC=BE=10,DC=DE,易得AE=6,则OE=10-6=4,即可得到E点坐标;在Rt△ODE中,设DE=x,则OD=OC-DC=OC-DE=8-x,利用勾股定理可计算出x,再在Rt△BDE中,利用勾股定理计算出BD;(2)、以D、M、N为顶点作平行四边形DMND′,作出点B关于x轴对称点B′,则易得到B′的坐标,D′的坐标,然后利用待定系数法求出直线D′B′的解析式,令y=0,得-2x+12=0,确定N点坐标,也即可得到M点坐标.
(1)、∵四边形OABC为矩形, ∴BC=OA=10,AB=OC=8,
∵△BCD沿BD折叠,使点C恰好落在OA边E点上, ∴BC=BE=10,DC=DE,
在Rt△ABE中,BE=10,AB=8, ∴AE=6, ∴OE=10-6=4, ∴E点坐标为(4,0);
在Rt△ODE中,设DE=x,则OD=OC-DC=OC-DE=8-x, ∴x2=42+(8-x)2,解得x=5,
在Rt△BDE中, BD=![]() ;
;
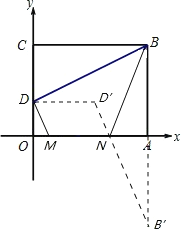
(2)、以D、M、N为顶点作平行四边形DMND′,作出点B关于x轴对称点B′,如图,
∴B′的坐标为(10,-8),DD′=MN=4.5,∴D′的坐标为(4.5,3),
设直线D′B′的解析式为y=kx+b,
把B′(10,-8),D′(4.5,3)代入得,10k+b=-8,4.5k+b=3,解得k=-2,b=12,
∴直线D′B′的解析式为y=-2x+12, 令y=0,得-2x+12=0,解得x=6,
∴M(1.5,0);N(6,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】据说,我国著名数学家华罗庚在一次访问途中,看到飞机邻座的乘客阅读的杂志上有一道智力题:一个数32768,它是一个正数的立方,希望求它的立方根,华罗庚不假思索给出了答案,邻座乘客非常惊奇,很想得知其中的奥秘,你知道华罗庚是怎样准确计算出的吗?请按照下面的问题试一试:
(1)由
 ,因为
,因为 ,请确定
,请确定 是______位数;
是______位数;(2)由32768的个位上的数是8,请确定
 的个位上的数是________,划去32768后面的三位数768得到32,因为
的个位上的数是________,划去32768后面的三位数768得到32,因为 ,请确定
,请确定 的十位上的数是_____________
的十位上的数是_____________(3)已知13824和
 分别是两个数的立方,仿照上面的计算过程,请计算:
分别是两个数的立方,仿照上面的计算过程,请计算: =____;
=____;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,要得到△ABD≌△ACE,从下列条件中补选一个,则错误的是( )

A.AB=AC B.DB=EC C.∠ADB=∠AEC D.∠B=∠C
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将1,
 ,
,  ,
,  按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,2)表示的两数之积是 _________.
按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,2)表示的两数之积是 _________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ABC=∠DCB,添加一个条件,使△ABC≌△DCB,你添加的条件是_____.(注:只需写出一个条件即可)

-
科目: 来源: 题型:
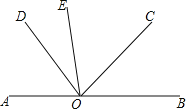
查看答案和解析>>【题目】如图,已知,A、O、B在同一条直线上,∠AOE=∠COD,∠EOD=30°.
(1)若∠AOE=88°30′,求∠BOC的度数;
(2)若射线OC平分∠EOB,求∠BOC的度数.
相关试题

