【题目】为了更好地治理水质,保护环境,某污水处理公司决定购买10台污水处理设备,现有A、B两种设备可供选择,月处理污水分别为240m3/月、200m3/月.经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少8万元.
(1)A、B两种型号的设备每台的价格是多少?
(2)若污水处理公司购买设备的预算资金不超过125万元,你认为该公司有哪几种购买方案?
(3)若每月需处理的污水约2040m3,在不突破(2)中资金预算的前提下,为了节约资金,又要保证治污效果,请你为污水处理公司设计一种最省钱的方案.
参考答案:
【答案】(1) 每台A型设备和每台B型设备各需要14万元、12万元;(2) ①A型设备1台,B型设备9台;②A型设备2台,B型设备8台;③A型设备0台,B型设备10台;(3) 公司购买方案A型设备1台,B型设备9台第一种方案最省钱
【解析】
(1)设每台A型设备和每台B型设备各需要x万元、(x-2)万元,由题意得:购买3台B型设备-购买2台A型设备比=8万元.根据等量关系列出方程,解方程即可;
(2)设应购置A型号的污水处理设备a台,则购置B型号的污水处理设备(10-a)台,由于要求资金不能超过125万元,即购买资金14a+12(10-a)≤125万元,根据不等关系列出不等式,再解不等式,求出非负整数解即可;
(3)设应购置A型号的污水处理设备m台,则购置B型号的污水处理设备(10-m)台,根据题中的不等关系可得关于m的不等式组,由此求出关于A型号处理机购买的几种方案,分类讨论,选择符合题意得那个方案即可.
(1)设每台A型设备和每台B型设备各需要x万元、(x-2)万元,
由题意得:3(x-2)-2x=8,
解得:x=14,
则x-2=12,
答:每台A型设备和每台B型设备各需要14万元、12万元;
(2)设应购置A型号的污水处理设备a台,则购置B型号的污水处理设备(10-a)台,
14a+12(10-a)≤125,
解得:a≤2.5,
∵a为非负整数,
∴a=0,1,2,
购买方案:①A型设备1台,B型设备9台;②A型设备2台,B型设备8台;③A型设备0台,B型设备10台;
(3)设应购置A型号的污水处理设备m台,则购置B型号的污水处理设备(10-m)台,
由题意得:![]() ,
,
解得:1≤m≤2.5,
∵m为整数,
∴m=1,2,
则B型购买的台数依次为9台,8台;
∵A型号的污水处理设备14万元一台,比B型的贵,
∴少买A型,多买B型的最省钱,
故买A型1台,B型9台,
答:该公司购买方案A型设备1台,B型设备9台第一种方案最省钱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲骑电瓶车,乙骑自行车从相距17km的两地相向而行.
(1)甲、乙同时出发经过0.5h相遇,且甲每小时行程是乙每小时行程的3倍少6km.求乙骑自行车的速度.
(2)若甲、乙骑行速度保持与(1)中的速度相同,乙先出发0.5h,甲才出发,问甲出发几小时后两人相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,点E,F在对角线AC上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,A、O、B在同一条直线上,∠AOE=∠COD,∠EOD=30°.
(1)若∠AOE=88°30′,求∠BOC的度数;
(2)若射线OC平分∠EOB,求∠BOC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张.

(1)请用树状图或列表的方法表示两次抽取卡片的所有可能出现的结果(卡片用A,B,C,D表示);
(2)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,求抽到的两张卡片上的数都是勾股数的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图8中图①,两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向
右平移到△A′B′D′的位置得到图②,则阴影部分的周长为_________

-
科目: 来源: 题型:
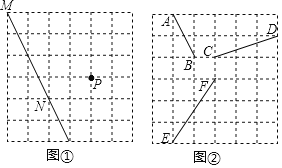
查看答案和解析>>【题目】如图,在6×6的正方形网格中,每个小正方形的边长为1,点A、B、C、D、E、F、M、N、P均为格点(格点是指每个小正方形的顶点).
(1)利用图①中的网格,过P点画直线MN的平行线和垂线.
(2)把图②网格中的三条线段AB、CD、EF通过平移使之首尾顺次相接组成一个三角形(在图②中画出三角形).
(3)第(2)小题中线段AB、CD、EF首尾顺次相接组成一个三角形的面积是______.
相关试题

