【题目】如图,在△ABC中,∠B=90°,AB=3,BC=2,点O在AC边上,⊙O与AB、BC分别切于点D、E,则⊙O的半径长为 . 
参考答案:
【答案】![]()
【解析】解:
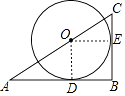
连接OE、OD,
∵⊙O与AB、BC分别切于点D、E,∠B=90°,
∴∠OEC=∠ODA=90°,∠ODB=∠B=∠OEB=90°,
∵OD=OE,
∴四边形OEBD是正方形,
∴OE=OD=DB=BE,
设OE=OD=DB=BE=R,
∵四边形OEBD是正方形,
∴OE∥AB,
∴∠COE=∠A,
∵∠OEC=∠ODA=90°,
∴△OEC∽△ADO,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:R= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】利用切线的性质定理和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将1,
 ,
,  ,
,  按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,2)表示的两数之积是 _________.
按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,2)表示的两数之积是 _________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ABC=∠DCB,添加一个条件,使△ABC≌△DCB,你添加的条件是_____.(注:只需写出一个条件即可)

-
科目: 来源: 题型:
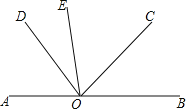
查看答案和解析>>【题目】如图,已知,A、O、B在同一条直线上,∠AOE=∠COD,∠EOD=30°.
(1)若∠AOE=88°30′,求∠BOC的度数;
(2)若射线OC平分∠EOB,求∠BOC的度数.
-
科目: 来源: 题型:
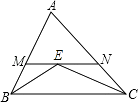
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB,AC于M、N,则△AMN的周长为( )
A.12
B.4
C.8
D.不确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好地治理水质,保护环境,某污水处理公司决定购买10台污水处理设备,现有A、B两种设备可供选择,月处理污水分别为240m3/月、200m3/月.经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少8万元.
(1)A、B两种型号的设备每台的价格是多少?
(2)若污水处理公司购买设备的预算资金不超过125万元,你认为该公司有哪几种购买方案?
(3)若每月需处理的污水约2040m3,在不突破(2)中资金预算的前提下,为了节约资金,又要保证治污效果,请你为污水处理公司设计一种最省钱的方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据要求进行计算:
(1)计算:(﹣1)5+15×3﹣2﹣ ;
;
(2)求不等式组: 的所有整数解.
的所有整数解.
相关试题

