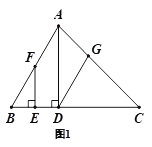
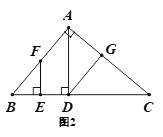
【题目】已知,在三角形ABC中,AD⊥BC于D,F是AB上一点,FE⊥BC于E,∠ADG=∠BFE
(1)如图1,求证:DG∥AB
(2)如图2,若∠BAC=90°,请直接写出图中与∠CAD互余的角,不需要证明.
参考答案:
【答案】(1)证明见解析;(2)∠BAD,∠BFE,∠ADG,∠C.
【解析】
(1) 根据AD⊥BC,FE⊥BC得AD∥EF,从而∠BFE=∠BAD,又∠ADG=∠BFE得∠BAD=∠ADG,根据平行线的判定得DG∥AB;
(2)根据互余的定义可得结论.
(1)证明:∵AD⊥BC,FE⊥BC
∴∠DAB=∠FEB=90°
∴AD∥EF
∴∠BFE=∠BAD
∵∠ADG=∠BFE
∴∠BAD=∠ADG
∴DG∥AB
(2) ∠BAD,∠BFE,∠ADG,∠C
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在平面直角坐标系中,作出下列各点,A(-3,4), B(-3,-2),O(0,0),并把各点连起来.
(2)画出△ABO先向下平移2个单位,再向右平移4 个单位得到的图形△A1B1o1,并直接写出A1坐标
(3) 直接写出三角形ABO的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+6x+c(a≠0)交y轴于A点,交x轴于B、C两点(点B在点C的左侧),已知A点坐标为(0,﹣5),点B的坐标为(1,0).
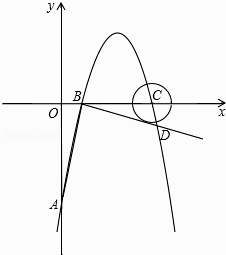
(1)求此抛物线的解析式及定点坐标;
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴与⊙C的位置关系,并说明理由;
(3)在抛物线上是否存在一点P,使△ACP是以AC为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,以每秒2cm的速度沿线段AB向点B方向运动,点Q从点D出发,以每秒3cm的速度沿线段DC向点C运动,已知动点P、Q同时出发,点P到达B点或点Q到达C点时,P、Q运动停止,设运动时间为t (秒).
(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求t的值;
(3)在点P、点Q的运动过程中,是否存在某一时刻,使得PQ⊥AB?若存在,请求出t的值并说明理由;若不存在,请说明理
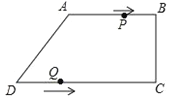

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE ≌ △CDF,则添加的条件不能为( )
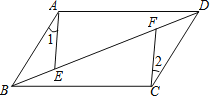
A. BE=DF B. BF=DE C. ∠1=∠2 D. AE=CF
-
科目: 来源: 题型:
查看答案和解析>>【题目】冰封超市购进一批运动服,按进价提高40%后标价,为了让利于民,增加销量,超市决定打八折出售,这时每套运动服的售价为140元.
(1)求每套运动服的进价?
(2)超市卖出一半后,正好赶上双十一促销,商店决定将剩下的运动服每3套400元的价格出售,很快销售一空,这批运动服超市共获利14000元,求该超市共购进多少套运动服?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了从甲、乙两名学生中选拨一人参加射击比赛,对他们的射击水平进行了测验,两人在相同条件下各射靶6次,命中的环数如下:
甲:7,8,6,10,10,7
乙:7, 7,8,8,10,8,
如果你是教练你会选拨谁参加比赛?为什么?
相关试题

