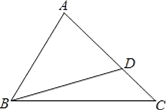
【题目】如图:△ABC中,∠C=45°,点D在AC上,且∠ADB=60°,AB为△BCD外接圆的切线.
(1)用尺规作出△BCD的外接圆(保留作图痕迹,可不写作法);
(2)求∠A的度数;
(3)求![]() 的值.
的值.
参考答案:
【答案】(1)作图见解析;(2)∠A=75°;(3)![]() =2.
=2.
【解析】试题分析:(1)利用三角形外接圆的圆心是各边垂直平分线的交点即可画出图形.
(2)只要证明△BOD是等腰直角三角形即可推出∠ABD=∠DBO=45°,利用三角形内角和定理即可解决问题.
(3)过点B作BE⊥AC,垂足为点E,设DE=x,则BD=2x,BE=![]() =
=![]() x,用x的代数式表示AD、DC即可解决问题.
x,用x的代数式表示AD、DC即可解决问题.
试题解析:(1)作BC的垂直平分线MN,作BD的垂直平分线HF,MN与FH的交点为O,以点O为圆心OB为作⊙O即可.如图所示:
;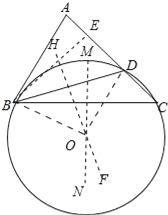
(2)连结OB、OD,
由切线性质,知∠ABO=90°.
∵∠ACB=45°,∴∠BOD=90°(同弧所对的圆周角等于它所对的圆心角的一半).
∵OB=OD,∴∠OBD=∠ODB=45°,
由∠ABO=90°,得∠ABD=45°,∴∠A=180°﹣∠ABD﹣∠ADB=180°﹣45°﹣60°=75°;
(3)过点B作BE⊥AC,垂足为点E,
在Rt△BCE中,∵∠ACB=45°,∴∠EBC=45°,∴BE=CE.
在Rt△BDE中,∵∠DBE=90°﹣∠EDB=30°,∴BD=2DE,
设DE=x,则BD=2x,BE=![]() =
=![]() xDC=CE﹣DE=BE﹣DE=(
xDC=CE﹣DE=BE﹣DE=(![]() ﹣1)x.
﹣1)x.
AE=AD﹣DE=AD﹣x.
在△ABC和△ADB中,∵∠ABD=∠ACB=45°,∠A为公共角,∴△ABC∽△ADB,
∴![]() ,即AB2=ACAD,即
,即AB2=ACAD,即
AB2=(AD+DC)AD=AD2+AD(![]() ﹣1)x ①.
﹣1)x ①.
在Rt△ABE中,由勾股定理,得AB2=AE2+BE2=(AD﹣x)2+(![]() x)2 ②.
x)2 ②.
由①、②,得AD2+AD(![]() ﹣1)x=(AD﹣x)2+(
﹣1)x=(AD﹣x)2+(![]() x)2,
x)2,
化简整理,解得AD=2(![]() ﹣1)x.
﹣1)x.
∴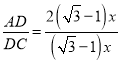 =2,
=2,
∴![]() =2.
=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的多项式x2﹣mx+n能因式分解为:(x﹣2)(x+3),则m+n=_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是平面直角坐标系及其中的一条直线,该直线还经过点C(3,﹣10).
(1)求这条直线的解析式;
(2)若该直线分别与x轴、y轴交于A、B两点,点P在x轴上,且S△PAB=6S△OAB,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,一次函数y=kx+3的图象经过点A(1,4).
(1)求这个一次函数的解析式;
(2)试判断点B(-1,5),C(0,3),D(2,1)是否在这个一次函数的图象上.

-
科目: 来源: 题型:
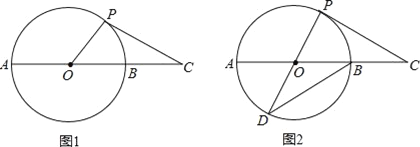
查看答案和解析>>【题目】如图1,延长⊙O的直径AB至点C,使得BC=
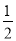 AB,点P是⊙O上半部分的一个动点(点P不与A、B重合),连结OP,CP.
AB,点P是⊙O上半部分的一个动点(点P不与A、B重合),连结OP,CP.(1)∠C的最大度数为 ;
(2)当⊙O的半径为3时,△OPC的面积有没有最大值?若有,说明原因并求出最大值;若没有,请说明理由;
(3)如图2,延长PO交⊙O于点D,连结DB,当CP=DB时,求证:CP是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有三张分别标有1、2、3数字的卡片(卡片除数字外完全相同).
(1)从袋中任意抽取一张卡片,则抽出的是偶数的概率为 ;
(2)从袋中任意抽取二张卡片,求被抽取的两张卡片构成两位数是奇数的概率.
-
科目: 来源: 题型:
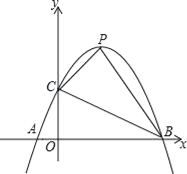
查看答案和解析>>【题目】已知,如图,抛物线y=﹣x2+ax+b与x轴从左至右交于A、B两点,与y轴正半轴交于点C.设∠OCB=α,∠OCA=β,且tanα﹣tanβ=2,OC2=OAOB.
(1)△ABC是否为直角三角形?若是,请给出证明;若不是,请说明理由;
(2)求抛物线的解析式;
(3)若抛物线的顶点为P,求四边形ABPC的面积.
相关试题

