【题目】在一个不透明的袋子中装有三张分别标有1、2、3数字的卡片(卡片除数字外完全相同).
(1)从袋中任意抽取一张卡片,则抽出的是偶数的概率为 ;
(2)从袋中任意抽取二张卡片,求被抽取的两张卡片构成两位数是奇数的概率.
参考答案:
【答案】(1)![]() ;(2)P(奇数)=
;(2)P(奇数)=![]() .
.
【解析】试题分析:(1)求出1,2,3三个数中偶数的个数,再直接根据概率公式求解即可;
(2)分别列举出可能组成的两位数,再根据概率公式解答即可.
试题解析:(1)随机地抽取一张,所有可能出现的结果有3个,每个结果发生的可能性都相等,其中卡片上的数字为偶数的结果有1个.
故从袋中任意抽取一张卡片,则抽出的是偶数的概率为: ![]() ;
;
故答案为: ![]() ;
;
(2)解法一:列举法
被抽取的两张卡片所有可能是:1、2;1、3;2、3.
而每一种情况,都可构成两个两位数,
即是:12,21,13,31,23,32,
共6个两位数.其中是奇数的为:
21,13,31,23共4个,
∴P(奇数)=![]() =
=![]() .
.
解法二:列表法
1 | 2 | 3 | |
1 | 12 | 13 | |
2 | 21 | 23 | |
3 | 31 | 32 |
从表中看出,共有6个两位数,
其中是奇数的为:13,21,23,31共4个,
∴P(奇数)=![]() =
=![]() .
.
解法三:树状图法

由树状图可知,构成的两位数共有6个,
分别是:12,13,21,23,31,32,
其中是奇数的为:13,21,23,31共4个,
∴P(奇数)=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,一次函数y=kx+3的图象经过点A(1,4).
(1)求这个一次函数的解析式;
(2)试判断点B(-1,5),C(0,3),D(2,1)是否在这个一次函数的图象上.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:△ABC中,∠C=45°,点D在AC上,且∠ADB=60°,AB为△BCD外接圆的切线.
(1)用尺规作出△BCD的外接圆(保留作图痕迹,可不写作法);
(2)求∠A的度数;
(3)求
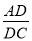 的值.
的值.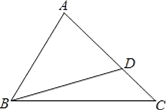
-
科目: 来源: 题型:
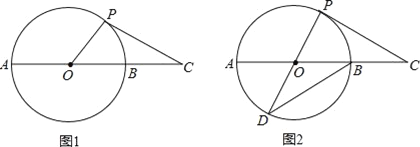
查看答案和解析>>【题目】如图1,延长⊙O的直径AB至点C,使得BC=
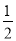 AB,点P是⊙O上半部分的一个动点(点P不与A、B重合),连结OP,CP.
AB,点P是⊙O上半部分的一个动点(点P不与A、B重合),连结OP,CP.(1)∠C的最大度数为 ;
(2)当⊙O的半径为3时,△OPC的面积有没有最大值?若有,说明原因并求出最大值;若没有,请说明理由;
(3)如图2,延长PO交⊙O于点D,连结DB,当CP=DB时,求证:CP是⊙O的切线.
-
科目: 来源: 题型:
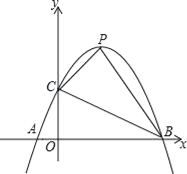
查看答案和解析>>【题目】已知,如图,抛物线y=﹣x2+ax+b与x轴从左至右交于A、B两点,与y轴正半轴交于点C.设∠OCB=α,∠OCA=β,且tanα﹣tanβ=2,OC2=OAOB.
(1)△ABC是否为直角三角形?若是,请给出证明;若不是,请说明理由;
(2)求抛物线的解析式;
(3)若抛物线的顶点为P,求四边形ABPC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若m2+n2﹣2m+4n+5=0.则m﹣n=_____.
-
科目: 来源: 题型:
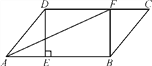
查看答案和解析>>【题目】如图,在ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的平分线.
相关试题

