【题目】如图是平面直角坐标系及其中的一条直线,该直线还经过点C(3,﹣10).
(1)求这条直线的解析式;
(2)若该直线分别与x轴、y轴交于A、B两点,点P在x轴上,且S△PAB=6S△OAB,求点P的坐标.

参考答案:
【答案】(1)直线的解析式为:y=﹣3x﹣1;(2)点P的坐标为P(![]() ,0)或P(﹣
,0)或P(﹣![]() ,0).
,0).
【解析】试题分析:(1)待定系数法求解可得;
(2)先根据直线解析式求得A、B点坐标,进而可得S△OAB=![]() ,设点P的坐标为P(m,0),用含m的式子表示出S△PAB,根据S△PAB=6S△OAB可得关于m的方程,解方程即可得.
,设点P的坐标为P(m,0),用含m的式子表示出S△PAB,根据S△PAB=6S△OAB可得关于m的方程,解方程即可得.
试题解析:(1)设直线的解析式为:y=kx+b,
由图可知,直线经过点(﹣1,2),
又已知经过点C(3,﹣10),
分别把坐标代入解析式中,得: ![]() ,解得
,解得![]() ,
,
∴直线的解析式为:y=﹣3x﹣1;
(2)由y=﹣3x﹣1,令y=0,
解得x=﹣![]() ;
;
令x=0,解得y=﹣1.
∴A、B两点的坐标分别为A(﹣![]() ,0)、B(0,﹣1).
,0)、B(0,﹣1).
S△OAB=![]() OAOB=
OAOB=![]() ×
×![]() ×1=
×1=![]() .
.
设点P的坐标为P(m,0),
则S△PAB=![]() PAOB=
PAOB=![]() ×|m﹣(﹣
×|m﹣(﹣![]() )|×1=
)|×1=![]() |m+
|m+![]() |,
|,
由S△PAB=6S△OAB,得![]() |m+
|m+![]() |=6×
|=6×![]() ,
,
从而得m+![]() =2或m+
=2或m+![]() =﹣2,
=﹣2,
∴m=![]() 或m=﹣
或m=﹣![]() ,
,
即点P的坐标为P(![]() ,0)或P(
,0)或P(![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB∶OE=3∶2.其中正确结论的个数是( )
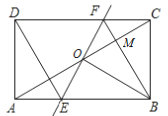
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.3a+b=3ab
B.3a﹣a=2
C.2a3+3a2=5a5
D.﹣a2b+2a2b=a2b -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的多项式x2﹣mx+n能因式分解为:(x﹣2)(x+3),则m+n=_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,一次函数y=kx+3的图象经过点A(1,4).
(1)求这个一次函数的解析式;
(2)试判断点B(-1,5),C(0,3),D(2,1)是否在这个一次函数的图象上.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:△ABC中,∠C=45°,点D在AC上,且∠ADB=60°,AB为△BCD外接圆的切线.
(1)用尺规作出△BCD的外接圆(保留作图痕迹,可不写作法);
(2)求∠A的度数;
(3)求
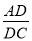 的值.
的值.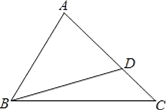
-
科目: 来源: 题型:
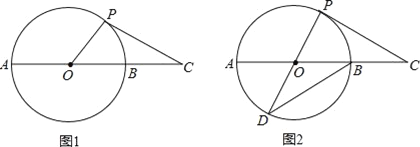
查看答案和解析>>【题目】如图1,延长⊙O的直径AB至点C,使得BC=
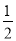 AB,点P是⊙O上半部分的一个动点(点P不与A、B重合),连结OP,CP.
AB,点P是⊙O上半部分的一个动点(点P不与A、B重合),连结OP,CP.(1)∠C的最大度数为 ;
(2)当⊙O的半径为3时,△OPC的面积有没有最大值?若有,说明原因并求出最大值;若没有,请说明理由;
(3)如图2,延长PO交⊙O于点D,连结DB,当CP=DB时,求证:CP是⊙O的切线.
相关试题

