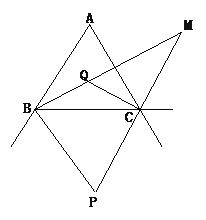
【题目】如图,△ABC的两外角平分线交于点P,易证∠P=90°-![]() ∠A;△ABC的两内角的平分线交于点Q,易证∠BQC=90°+
∠A;△ABC的两内角的平分线交于点Q,易证∠BQC=90°+![]() ∠A;那么△ABC的内角平分线BM与外角平分CM的夹角∠M=_____∠A.
∠A;那么△ABC的内角平分线BM与外角平分CM的夹角∠M=_____∠A.
参考答案:
【答案】![]()
【解析】
已知CQ、CM分别是∠ACB及其外角的平分线,可得∠QCM=90°,由题意可得∠BQC=90°+![]() ∠A,根据三角形外角的性质可得,∠BQC=∠QCM+∠M=90°+∠M,由此即可求得∠ A和∠M的关系.
∠A,根据三角形外角的性质可得,∠BQC=∠QCM+∠M=90°+∠M,由此即可求得∠ A和∠M的关系.
∵CQ、CM分别是∠ACB及其外角的平分线,
∴∠QCM=90°,
由题意可得∠BQC=90°+![]() ∠A,
∠A,
根据三角形外角的性质可得,∠BQC=∠QCM+∠M=90°+∠M,
∴90°+![]() ∠A=90°+∠M,
∠A=90°+∠M,
∴![]() ∠A=∠M.
∠A=∠M.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ACB中,∠ACB=90°,∠ABC的平分线BE和∠BAC的外角平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G.则下列结论:①∠APB=45°;②PF=PA;③BD﹣AH=AB;④DG=AP+GH.其中正确的是( )

A. ①②③ B. ①②④ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB=AC,AF⊥BC于点F,D、E分别为BF、CF的中点,则图中全等三角形共有____对.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是反比例函数y1=
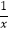 (x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2=
(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2= 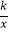 (x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为 .
(x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为 . 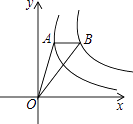
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是 (请将所有正确结论的序号都填上).

-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c(a≠0)图象的一部分如图所示,其对称轴为x=2,与x轴的一个交点是(﹣1,0),有以下结论:①abc>0;②4a﹣2b+c<0;③4a+b=0④抛物线与x轴的另一个交点是(5,0)⑤若点(﹣3,y1)(﹣6,y2)都在抛物线上,则y1<y2 . 其中正确的是 . (只填序号)
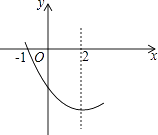
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A
 B
B C
C ;
;(2) 请画出△ABC关于原点对称的△A
 B
B C
C ;
;(3) 在
 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
相关试题

