【题目】如图所示,AB=AC,AF⊥BC于点F,D、E分别为BF、CF的中点,则图中全等三角形共有____对.

参考答案:
【答案】4
【解析】
根据已知条件,利用HL证明Rt△ABF≌Rt△ACF,再由SAS证明△ADF≌△AEF,由SAS证明△ABD≌△ACE,由SAS证明△ABE≌△ACD,由此即可解答.
在△ABF与△ACF中,因为∠AFB=∠AFC=90°,AB=AC,AF为公共边,所以Rt△ABF≌Rt△ACF(HL),所以∠B=∠C,BF=CF.再由D、E分别是BF、FC的中点,得BD=DF=FE=EC.
在△ADF与△AEF中,因为DF=FE,∠AFD=∠AFE, AF=AF,所以△ADF≌△AEF(SAS).
在△ABD与△ACE中,因为AB=AC,∠B=∠C,BD=CE,所以△ABD≌△ACE(SAS).
在△ABE与△ACD中,因为AB=AC,∠B=∠C,BE=CD,所以△ABE≌△ACD(SAS),故有4对全等三角形.
故答案为:4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张老师驾车从家出发到植物园赏花,匀速行驶一段时间后,途中遇到堵车原地等待一会儿,然后加速行驶,到达植物园,参观结束后,张老师驾车一路匀速返回,其中x表示汽车从家出发后所用时间,y表示车离家的距离,下面能反映y与x的函数关系式的大致图象是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB⊥BE于点B,DE⊥BE于点E.
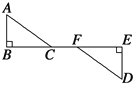
(1)若∠A=∠D,AB=DE,则△ABC与△DEF全等的理由是____;
(2)若∠A=∠D,BC=EF,则△ABC与△DEF全等的理由是_________;
(3)若AB=DE,BC=EF,则△ABC与△DEF全等的理由是_______;
(4)若AB=DE,AC=DF,则△ABC与△DEF全等的理由是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣2,﹣
 ,
,  ,1,3五个数中任选1个数,记为a,它的倒数记为b,将a,b代入不等式组
,1,3五个数中任选1个数,记为a,它的倒数记为b,将a,b代入不等式组  中,能使不等式组至少有两个整数解的概率是 .
中,能使不等式组至少有两个整数解的概率是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】将长方形纸片ABCD的一角沿AE折叠,使点D落在点D′处,得到如图所示的图形,若∠CED′=56°,则∠D′AB=_____度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,延长CB至M,使BM=2,连接AM,BN⊥AM于N,O是AC、BD的交点,连接ON,则ON的长为
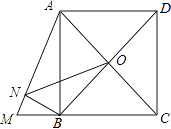
相关试题

