【题目】抛物线y=ax2+bx+c(a≠0)图象的一部分如图所示,其对称轴为x=2,与x轴的一个交点是(﹣1,0),有以下结论:①abc>0;②4a﹣2b+c<0;③4a+b=0④抛物线与x轴的另一个交点是(5,0)⑤若点(﹣3,y1)(﹣6,y2)都在抛物线上,则y1<y2 . 其中正确的是 . (只填序号) 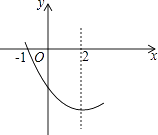
参考答案:
【答案】①③④⑤
【解析】解:①∵抛物线开口向下, ∴a<0,
∵对称轴是:x=2,
∴a、b异号,
∴b>0,
∵抛物线与y轴交于负半轴,
∴c<0,
∴abc>0,
∴选项①正确;
②由图象得:当x=﹣2时,y>0,
∴4a﹣2b+c>0,
∴选项②不正确;
③抛物线对称轴是:x=﹣ ![]() =2,
=2,
b=﹣4a,
4a+b=0,
∴选项③正确;
④由对称性得:抛物线与x轴的另一个交点为(5,0),
∴选项④正确;
⑤∵对称轴是:x=2,且开口向上,
∴当x<2时,y随x的增大而减小,
∵﹣3>﹣6,
∴y1<y2 ,
∴选项⑤正确;
所以答案是:①③④⑤.
【考点精析】关于本题考查的二次函数图象以及系数a、b、c的关系和抛物线与坐标轴的交点,需要了解二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c);一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是反比例函数y1=
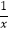 (x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2=
(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2= 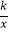 (x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为 .
(x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为 . 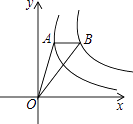
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的两外角平分线交于点P,易证∠P=90°-
 ∠A;△ABC的两内角的平分线交于点Q,易证∠BQC=90°+
∠A;△ABC的两内角的平分线交于点Q,易证∠BQC=90°+ ∠A;那么△ABC的内角平分线BM与外角平分CM的夹角∠M=_____∠A.
∠A;那么△ABC的内角平分线BM与外角平分CM的夹角∠M=_____∠A.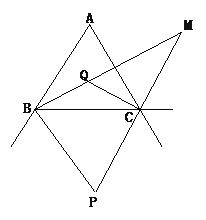
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是 (请将所有正确结论的序号都填上).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A
 B
B C
C ;
;(2) 请画出△ABC关于原点对称的△A
 B
B C
C ;
;(3) 在
 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.

(1)∠1与∠2有什么关系,为什么?
(2)BE与DF有什么关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到元购物券,至多可得到元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
相关试题

