搜索
【题目】如图，抛物线y1=a（x+2）2﹣3与y2=
（x﹣3）2+1交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于点B，C．则以下结论：
①无论x取何值，y2的值总是正数；
②a=1；
③当x=0时，y2﹣y1=4；
④2AB=3AC；
其中正确结论是（ ）
A. ①② B. ②③ C. ③④ D. ①④
参考答案：
【答案】D
【解析】试题解析：：①∵抛物线y2=
（x-3）2+1开口向上，顶点坐标在x轴的上方，∴无论x取何值，y2的值总是正数，故本结论正确；
②把A（1，3）代入，抛物线y1=a（x+2）2-3得，3=a（1+2）2-3，解得a=
，故本结论错误；
③由两函数图象可知，抛物线y1=a（x+2）2-3解析式为y1=
（x+2）2-3，当x=0时，y1=
（0+2）2-3=-
，y2=
（0-3）2+1=
，故y2-y1=
+
=
，故本结论错误；
④∵物线y1=a（x+2）2-3与y2=
（x-3）2+1交于点A（1，3），
∴y1的对称轴为x=-2，y2的对称轴为x=3，
∴B（-5，3），C（5，3）
∴AB=6，AC=4，
∴2AB=3AC，故本结论正确．
故选D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为加强中小学生安全和禁毒教育，某校组织了“防溺水、交通安全、禁毒”知识竞赛，为奖励在竞赛中表现优异的班级，学校准备从体育用品商场一次性购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格相同），购买1个足球和1个篮球共需159元；足球单价是篮球单价的2倍少9元．
（1）求足球和篮球的单价各是多少元？
（2）根据学校实际情况，需一次性购买足球和篮球共20个，但要求购买足球和篮球的总费用不超过1550元，学校最多可以购买多少个足球？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，点G是正方形ABCD对角线CA的延长线上任意一点，以线段AG为边作一个正方形AEFG，线段EB和GD相交于点H．
（1）求证：EB=GD且EB⊥GD；
（2）若AB=2，AG=
，求
的长；（3）如图2，正方形AEFG绕点A逆时针旋转
连结DE，BG，
与
的面积之差是否会发生变化？若不变，请求出与的面积之差；若变化，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】完成下面的推理．
如图，BE平分∠ABD，DE平分∠BDC，且∠α＋∠β＝90°，试说明：AB∥CD.
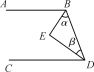
完成推理过程：
∵BE平分∠ABD(已知)，
∴∠ABD＝2∠α(__________)．
∵DE平分∠BDC(已知)，
∴∠BDC＝2∠β (__________)．
∴∠ABD＋∠BDC＝2∠α＋2∠β＝2(∠α＋∠β)( __________)．
∵∠α＋∠β＝90°(已知)，
∴∠ABD＋∠BDC＝180°(__________)．
∴AB∥CD(____________________)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知A（
，y1），B（2，y2）为反比例函数y=
图象上的两点，动点P（x，0）在x轴正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知
的边
平行于
轴，
点
的坐标为
，点
的坐标为
，点
在第四象限，点
是边上的一个动点．
（1）若点
在边
上，
求点的坐标；（2）若点
在边
或
上，点
是与
轴的交点如图2，过点作轴的平行线
过点作轴的平行线
它们相交于点
，将
沿直线
翻折，当点的对应点落在坐标轴上时，求点的坐标．(直接写出答案) -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
中，
，
．点
是射线
上一动点，过点
作射线
的垂线，垂足为点
，点
为
的中点，连结
，则的最小值为________．
相关试题
