搜索
【题目】如图，已知A（
，y1），B（2，y2）为反比例函数y=
图象上的两点，动点P（x，0）在x轴正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是_____．
参考答案：
【答案】（
，0）
【解析】试题解析：∵把A（
，y1），B（2，y2）代入反比例函数y=
得：y1=2，y2=
，
∴A（
，2），B（2， 
）．
在△ABP中，由三角形的三边关系定理得：|AP-BP|＜AB，
∴延长AB交x轴于P′，当P在P′点时，PA-PB=AB，
即此时线段AP与线段BP之差达到最大，
设直线AB的解析式是y=ax+b（a≠0）
把A、B的坐标代入得：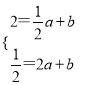 
，
解得：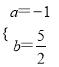 
，
∴直线AB的解析式是y=-x+
，
当y=0时，x=
，即P（
，0）；
故答案为：（
，0）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，点G是正方形ABCD对角线CA的延长线上任意一点，以线段AG为边作一个正方形AEFG，线段EB和GD相交于点H．
（1）求证：EB=GD且EB⊥GD；
（2）若AB=2，AG=
，求
的长；（3）如图2，正方形AEFG绕点A逆时针旋转
连结DE，BG，
与
的面积之差是否会发生变化？若不变，请求出与的面积之差；若变化，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】完成下面的推理．
如图，BE平分∠ABD，DE平分∠BDC，且∠α＋∠β＝90°，试说明：AB∥CD.
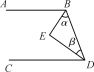
完成推理过程：
∵BE平分∠ABD(已知)，
∴∠ABD＝2∠α(__________)．
∵DE平分∠BDC(已知)，
∴∠BDC＝2∠β (__________)．
∴∠ABD＋∠BDC＝2∠α＋2∠β＝2(∠α＋∠β)( __________)．
∵∠α＋∠β＝90°(已知)，
∴∠ABD＋∠BDC＝180°(__________)．
∴AB∥CD(____________________)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y1=a（x+2）2﹣3与y2=
（x﹣3）2+1交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于点B，C．则以下结论：①无论x取何值，y2的值总是正数；
②a=1；
③当x=0时，y2﹣y1=4；
④2AB=3AC；
其中正确结论是（ ）
A. ①② B. ②③ C. ③④ D. ①④
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知
的边
平行于
轴，
点
的坐标为
，点
的坐标为
，点
在第四象限，点
是边上的一个动点．
（1）若点
在边
上，
求点的坐标；（2）若点
在边
或
上，点
是与
轴的交点如图2，过点作轴的平行线
过点作轴的平行线
它们相交于点
，将
沿直线
翻折，当点的对应点落在坐标轴上时，求点的坐标．(直接写出答案) -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
中，
，
．点
是射线
上一动点，过点
作射线
的垂线，垂足为点
，点
为
的中点，连结
，则的最小值为________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在读书月活动中，学校准备购买一批课外读物．为使课外读物满足同学们的需求，学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查（每位同学只选一类），如图是根
据调查结果绘制的两幅不完整的统计图．
请你根据统计图提供的信息，解答下列问题：
（1）本次调查中，一共调查了 名同学；
（2）条形统计图中，m= ，n= ；
（3）扇形统计图中，艺术类读物所在扇形的圆心角是 度；
（4）学校计划购买课外读物6000册，请根据样本数据，估计学校购买其他类读物多少册比较合理？
相关试题
